Теорема лапласа. (Метод рекурентных соотношений)

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. Пример , приведенный ниже показывает по разложение по первой строке.

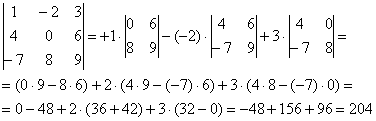
Свойства определителей:

1. Если у определителя какая-либо строка (столбец) состоит из нулей, то Определитель (ОПР) = 0 2. Если 2 строки (столбца) пропорциональны, то Опр = 0 3. Если 2 строки (2 столбца) поменять местами, то определитель изменит знак. 4. Если строку (столбец) умножить на число, то и Опр умножится на это число. Эти может и не нужно доказывать , но написать мне их нужно. 5. Если к одной строке (столбцу) прибавить другую строку (столбец) , помноженную на число, то Опр не изменится. 6. Опр произведения матриц равен произведению их Опр-й. 7. Опр транспонированной м. равен Опр самой матрицы 8. Если строку (столбец) умножить на алгеброическое дополнения другой строки (столбца), то полученная сумма будет равна 0 9. Опр треугольной матрицы равен произведению диагональных элементов.

ДОКАЗАТЬ СВОЙСТВА!!!

Вопрос 4. Обратная матрица. Метод присоединенной матрицы и метод элементарных преобразований.

Обратная матрица - это такая матрица, при умножении на которую, исходная матрица дает в результате единичную матрицу.

Обратную матрицу   можно найти по следующей формуле:

, где   – определитель матрицы  ,   – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .

Понятие обратной матрицы существует только для квадратных матриц.

В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

Минор – это определитель, составленный из первоночального определителя, путем вычеркивания k-строк и k- любых столбцов.

Алгебраическим дополнением  А_ij  элемента а_ij матрицы  n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

ДОК-ВО МЕТОД ПРИСОЕДИНЕЕНОЙ И ЭЛЕМЕНТАРНЫМИ ПРЕОБРАЗОВАНИЯМИ.

Вопрос 5. Теорема о Ранге матрице.

Рангом матрицы называется максимальная размерность его не нулевого минора.

Теорема. Ранг матрицы совпадает с максимальной количеством её линейных независимых строк (столбцов).

Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

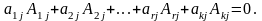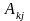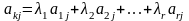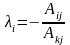Поскольку является базисным минором, поэтому, разделив полученное равенство на , найдем, что для всех j=1,2,…,n, где . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана