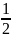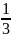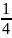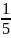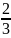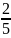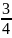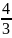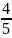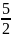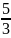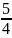- •Вопрос 1. Аксиомы поля. Поле комплексных чисел. Запись комплексного числа.
- •1)Коммутативность сложения и умножения.
- •2)Умножения
- •3)Ассоциативность
- •Вопрос 2.Кольцо матриц над полем действительных чисел. Основные операции над матрицами. Свойства операций.
- •Сложение (вычитание) матриц – складывать (вычитать) по элементам и только над матрицами одинаковой размерности.
- •Умножение матрицы на число , произведение.
- •Коммуникативность:
- •Ассоциативность:
- •Вопрос 3. Определители. Теорема Лапласа. Свойства определителей.
- •Теорема лапласа. (Метод рекурентных соотношений)
- •Вопрос 4. Обратная матрица. Метод присоединенной матрицы и метод элементарных преобразований.
- •Вопрос 5. Теорема о Ранге матрице.
- •Вопрос 6. Теорема Кронекера-Капелли
- •Достаточность
- •Вопрос 7. Решение слу. Метод Крамера, матричный метод, метод Гауса
- •Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •Вопрос 8.Однородные слу. Построение фундаментальной системы решений
- •Вопрос 9. Векторы. Основные понятия. Скалярное произведение, его свойства
- •Вопрос 10. Векторное произведение векторов. Свойства.
- •Вопрос 11. Смешанное произведение. Свойства
- •Вопрос 12. Преобразование координат на плоскости. Парралельный перенос. Поворот.
- •Вопрос 13. Кривые второго порядка.Каноническое уравнение эллипса.
- •Эллипс.
- •Вопрос 14. Кривые второго порядка.Каноническое уравнение параболы и гиперболы.
- •Парабола.
- •Вопрос 15. Классификация кривых 2-го порядка.Приведение к каноническому виду. Кривая второго порядка может быть задана уравнением
- •Вопрос 16. Плоскость в пространстве. Основные типы уравнений плоскости.
- •Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
- •Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .
- •Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.
- •Вопрос 17. Прямая в пространстве. Основные типы уравнений.
- •Уравнение прямой в пространстве, проходящей
- •Вопрос 18. Метод сечений в пространстве.Эллипсоиды и гиперболоиды.(с примерами).
- •Цилиндрические поверхности.
- •Гиперболоид.
- •Вопрос 19. Метод сечений.Цилиндры и Конусы.(с примерами).
- •Цилиндр
- •Вопрос 20. Линейные пространства.Основные понятия.Теорема о Базисе.
- •Вопрос 21. Матрица перехода от Базиса к Базису.
- •Вопрос 22. Линейный оператор и его матрица.
- •Вопрос 23. Собственные значения и собственные векторы линейных операторов.
- •Вопрос 24.Приведение уравнения 2-го порядка к каноническому виду(Алгоритм, с примером).
- •Вопрос 25.Множество операций над множеством.
- •Операции над множествами.
- •Вопрос 26.Докозательсво , что множество действительных числе не .
- •Вопрос 27. Функция, последовательность, их пределы (примеры бесконечно малых и больших последовательностей).
- •Вопрос 28. Теорема о пределе монотонной ограниченной последовательности, теорема о пределе промежуточной функции.
- •Вопрос 32.Неопределенности.Сравнение бесконечно малых. Таблица эквивалентности.
Вопрос 26.Докозательсво , что множество действительных числе не .
Начнем
двигаться из левого верхнего угла
таблицы и нумеровать дроби по порядку,
исключая те, которые встречались ранее.

0 |
1 |
2 |
3 |
4 |
5 |
1 |
1 |
|
|
|
|
2 |
2 |
1 |
|
|
В
этой таблице нашим способом можно
дойти до любого рационального числа.
При этом каждому рациональному числу
соответствует его натуральный номер.
Таким образом между положительными
рациональными числами и натуральными
числами установлено взаимно однозначное
соответствие. Они равномощны.
|
3 |
3 |
|
1 |
|
|
4 |
4 |
2 |
|
1 |
|
5 |
5 |
|
|
|
1 |
… |
… |
… |
… |
… |
… |
С рациональными отрицательными числами установлено взаимно-однозначное соответствие таким же образом, как между натуральными и целыми.
Множество действительных чисел несчетные.
1
0


В этом множестве любое число записывается десятичной дробью, в которой после нуля следует любая бесконечная последовательность цифр от 0 до 9, за исключение последовательностей, начиная с нечетного элемента (0,99999…9=1)
Рассмотрим
последовательность, в котором на i-ом
месте стоит цифра, отличная от i-ой
цифры i-ого числа и 9.

1 |
0,000…0… |
2 |
0,010…0… |
3 |
0,1111…0… |
4 |
0,12345… |
5 |
0,121241…. |
… |
… |
0,12267 – данная последовательность не совпадает ни с одной из последовательностей, вписанных в столбец, поскольку в i-ой последовательности она отличается в i-ом знаке и поэтому не будет пронумерована. И значит, множество действительных чисел неравномощно счетному множеству.
Вопрос 27. Функция, последовательность, их пределы (примеры бесконечно малых и больших последовательностей).
E(t)
– область значений
D(t)
– область
определения




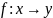
Функция переводящая в натуральный ряд в множество У называется последовательностью.
4
3
2
1




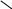
 ,
при этом
,
при этом
 ее
можно задавать двумя способами: словесно
и с помощью
ее
можно задавать двумя способами: словесно
и с помощью
графика.
 Предел
функции:
Предел
функции:
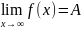
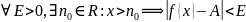
 Пример:
Пример:
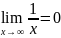 – гипербол
– гипербол
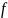
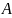
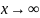
0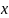
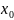
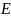
для
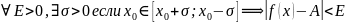
Предел
последовательности: пределом
последовательности
называется число А и символ
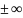 ,
тогда и только тогда, когда:
,
тогда и только тогда, когда:
предел
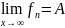 тогда и только тогда, когда для
тогда и только тогда, когда для
 ,
,
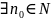 ,
что из
,
что из
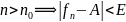 ;
;
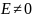
предел
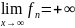
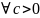 ,
,
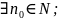



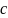
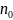
Последовательность ![]() называется бесконечно
малой,
если
называется бесконечно
малой,
если ![]() .
Например, последовательность чисел
.
Например, последовательность чисел ![]() —
бесконечно малая
—
бесконечно малая
Функция
называется бесконечно
малой в окрестности точки ![]() ,
если
,
если ![]()
Последовательность
называется бесконечно
большой,
если ![]()
Функция
называется бесконечно
большой в окрестности точки
,
если ![]()