Ответы по математике экзамен.

Вопрос 1. Аксиомы поля. Поле комплексных чисел. Запись комплексного числа.

Одной из причин расширения понятия числа является потребность в решении уравнений. В множестве натуральных чисел N неразрешимо даже такое простейшее уравнение, как x + 1 = 0, в множестве целых чисел Z уравнение 2x = 1, в множестве рациональных чисел Q уравнение x² = 2. В множестве действительных чисел R все эти уравнения имеют решение, но остается неразрешимым такое простое уравнение, как, например, x² + 1 = 0. В множестве комплексных чисел C это уравнение разрешимо. В множестве C разрешимо любое алгебраическое уравнение с одним неизвестным.

Определение.

Комплексным числом называется упорядоченная пара (a;b) действительных чисел a и b. Числа (a;b) и (c;d) называются равными, если a = c и b = d. Действительное число a называется действительной частью числа (a;b), а действительное число b - мнимой частью числа (a;b). Суммой комплексных чисел (a;b) и (c;d) называется число (a + c;b + d), а их произведением - число (ac-bd;ad + bc). Множество всех комплексных чисел обозначается через C.

Правила:

1. Комплексное число (0;1) называется мнимой единицей и обозначается через i.

По определению умножения комплексных чисел

i² = (0;1) × (0;1) = (-1;0) , отсюда следует что i²=-1.

2) Заметим, что

(a;b) = (a;0) + (0;b) = (a;0) + (b;0) × (0;1) = a + bi

Выражение a + bi называется алгебраической формой комплексного числа (a; b).

3) Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

Т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

Операции над комплексными числами:

1) Правило сложения и вычитания комплексных чисел. С примером.

(a+bi)+(c+di)=(a+c)+(b+d)i Пример : 1+i+3+7i=4+8i

Нулем комплексных чисел является : 0+0i=0 1+i+0+0i=1+i

2)Правило умножения.

(a+bi)*(c+di)=(ac-bd)+(ad+bc)i Пример : (1+i)*(3-2c)=(3+2)*(-2+3)i=5+i

3)Правило деления.

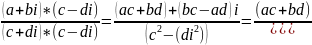
Операция деления не возможна, если c,d=0

Множество комплексных чисел является полем.

1)Коммутативность сложения и умножения.

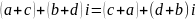
2)Умножения

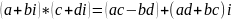
3)Ассоциативность

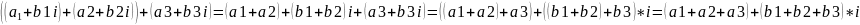
Если проссумируем выражение расставив скобки иначе, то результат будет такой же.

Ассоциативность умножения.

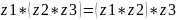
Z1=a1+b1i

Z2=a2+b2i

Z3=a3+b3i

4) Дистрибутивность умножения относительно сложения

z1(z2+z3)=z1*z2+z1*z3

5)Наличие нуля и единицы.

0+0i*(a+bi)= (0a-0b)+(0b+0a)i=0 – мультипротикативый ноль.

единицы :

(1+0i)*(a+bi)=(1*a-0b)+(1*b+0a)i=a+bi

Тригометрическая запись числа.

Любое число z=a+bi можно на плоскости изобразить точкой , с координатами (a;b) a – x , b – y .

Любое комплексное число имеет свой аргумент Arg(z) (между осью абцисс и вектором)

Так же любое комплексное число имеет норму |z|.

r=|z| - длина его вектора

r=|z|=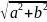

Любое комплексное число определяется своей нормой и аргументом, при этом 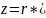– тригометрическая запись числа.

cosq= a/r , sinq = b/r

Модулем комплексного числа   называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Аргументом комплексного числа   называется угол   между положительной полуосьюдействительной оси   и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .