37. Проверка жесткости балок.

Прогибы не должны превышать предельных значений

f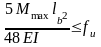 _max ≤ f_u

Балка настила является однопролетной, статически определимой с равномерно распределенной нагрузкой. Максимальный расчетный изгибающий момент в середине пролета балки определяется по формуле

38. Определение высоты составных балок.

Д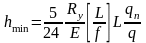 ля балки нагруженной равномерно распределенной нагрузкой минимальная высота находится из условия жесткости по формуле:

где q_n и q - соответственно нормативная и расчетная нагрузки;

R_y - расчетное сопротивление материла;

Е - модуль упругости стали (Е = 2.06104 MПа);

L - пролет балки;

f – предельный прогиб балки по СНиП 2.01.07-85*.

О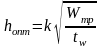 птимальная высота для составных балок определяется по формуле:

где k - коэффициент, принимаемый для сварных балок равным 1.15  1.20;

W_mр - требуемый момент сопротивления балок определяемый по условию прочности;

t_w - толщина стенки балки (при определении h_опт – задается в соответствии с таблицей)

1. Высоту балки следует принимать равной или близкой оптимальной, но не менее h_min.

2. Возможное отклонение от h_oпт следует делать в сторону уменьшения.

3. В целях унификации конструкций высота балки должна быть кратной 100 мм.

4. Следует стремиться к тому, чтобы высота стенки по возможности была равной ширине прокатного стального листа, чтобы исключить его продольную резку.

39. Определение толщины стенки составных балок.

М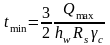 инимальная толщина стенки определяется из условия прочности на сдвиг (срез) стенки у опоры по формуле:

где R_s – расчетное сопротивление стали сдвигу.

40. Последовательность подбора сечения составных балок.

П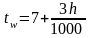 одбор сечения сварных составных балок производится в следующей последовательности:

1. задается ориентировочная высота балки h=(1/8…1/12);

2) определяется толщина стенки по эмпирической формуле:

где t_w и h в мм;

3) по наибольшему (расчетному) изгибающему моменту M_max находится требуемый момент сопротивления балки;

4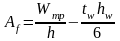 ) определятся высота балки, исходя из экономических соображений h_опт и требований по второму предельному состоянию h_min;

5) определятся площадь поперечного сечения поясов A_f:

6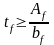 ) задается ширина пояса в пределах b_f = (1/3...1/5)h (из условия общей устойчивости балки);

7) определяется толщина пояса

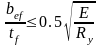
Отношение ширины свеса b_ef и t_f должно быть

8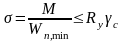 ) вычисляется момент инерции I_x и момент сопротивления W_x подобранного сечения балки;

9) выполняются проверки:

- прочности по нормальным напряжениям

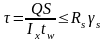( недонапряжение допускается не более 5%, перенапряжение не допускается);

- прочности стенки на сдвиг (срез) торцевом опорном ребре

41. Обеспечение местной и общей устойчивости балок.

О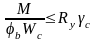 бщая устойчивость

Обеспеченность общей устойчивости балок проверяется по формуле:

где Wc - момент сопротивления наиболее сжатого волокна пояса в плоскости наибольшего изгибающего момента;

jb – коэффициент, учитывающий снижение расчетных напряжений вследствие потери балки общей устойчивости, определяемой по прил. 7 СНиП II-23-81*;

Если в результате проверки общая устойчивость не обеспечена, то необходимо увеличить ширину поясов или установить горизонтальные связи.

Проверка устойчивости балки не требуется в следующих случаях:

1. При передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки;

2. При отношении расчетной длины Lef к ширине пояса bf, не превышающим значений, определяемых по СНиП II-23-81*.

Устойчивость стенки балки

Потеря устойчивости может произойти от критических нормальных, касательных или местных напряжений,которые определяется по формулам:

- критические нормальные напряжения

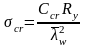
- критические касательные напряжения

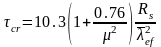
- критические местные напряжения

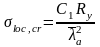
где

Сcr– коэффициент, принимаемый по табл. 21 СНиПII-23-81;

d – меньшая из сторон пластины;

а - расстояние между осями поперечных ребер жесткости;

m - отношение большей стороны пластины к меньшей;

С1 - коэффициент по табл. 23 СНиП II-23-81*;

h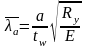 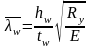w = hef - расчетная высота стенки;

tw = t – толщина стенки.

Условная гибкость стенки отсека

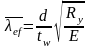
Условная приведенная гибкость стенки

Проверка местной устойчивости сводится к проверке условий:

- при действии нормальных напряжений s £ sсг;

- при действии касательных напряжений t £ tсг;

- при действии местных напряжений sloс £ sloc,cr

Напряжения s, t и sloc определяют:

- ecли а < hw в сечении a/2;

- если hw > a в сечении hw/2 от ребра (где больший изгибающий момент)

Касательные напряжения определяются как средние по сечению стенки балки, без учета работы поясов, по формуле:

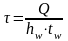
где Q – поперечная сила в расчетном сечении балки.

Нормальные напряжения определяются в стенке на уровне поясных швов по формуле:

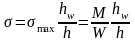
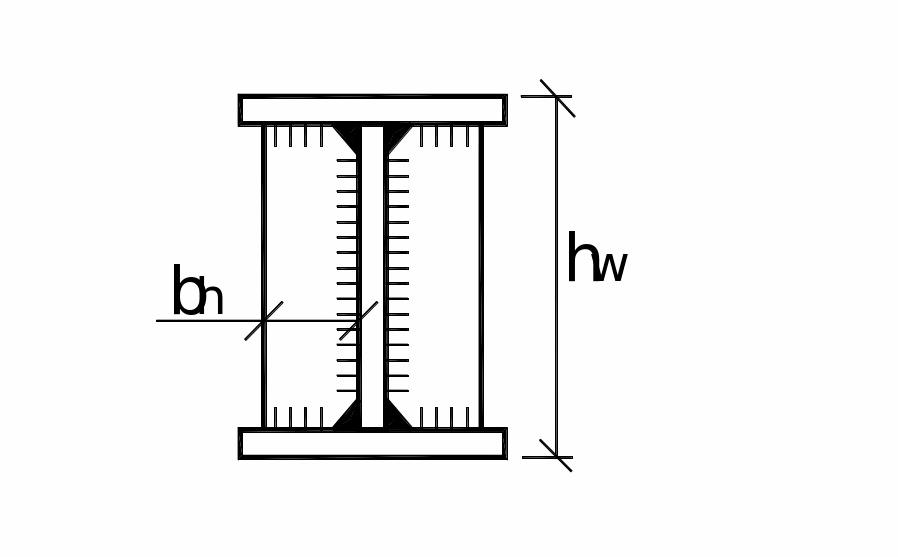
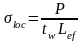
Местные напряжения от сосредоточенной нагрузки:

где P - сосредоточенная нагрузка;

tw – толщина стенки;

Lef = b + 2tf - условная длина распределения давлений сосредоточенной нагрузки P.

П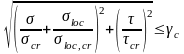 роверка местной устойчивости стенки балки симметричного сечения, укрепленной только поперечными ребрами жесткости, при совместном учете нормальных, касательных и местных напряжений, производится по формуле:

где gс – коэффициент условия работы;

s, t, sloc – действующие напряжения в рассматриваемой точке;

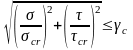scr, tcr, sloc,cr – соответствующие критические напряжения, определяемые по приведенным выше формулам и с учетом СНиП II-23-81*.

При sloc = 0 местная устойчивость стенки проверяется по формуле:

Стенки балки не следует укреплять поперечными ребрами жесткости, если значение условной гибкости:

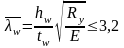
(при отсутствии подвижной нагрузки);

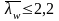
и (при наличии подвижной нагрузки на поясе балки)

Расстояние между поперечными ребрами не должно превышать:

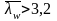
- 2hw при

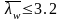
- 2.5hw при

Ш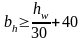 ирина выступающей части парного симметричного ребра принимается равной:

;

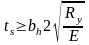
- толщина ребра:

Местную устойчивость стенок балок не требуется проверять, если условная гибкость стенки не превышает значений:

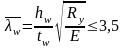
- при отсутствии местных напряжений (sloc = 0) в балках с двухсторонними поясными швами;

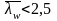
- при наличии местных напряжений (sloc ¹ 0).