6. Отражение и преломление акустических волн на границах раздела сред. Трансформация волн. Критические углы.
Рассмотрим случай, когда плоская упругая волна, распространяясь в среде 1, падает под произвольным углом на границу раздела. Геометрия задачи и направление координатных осей показаны на рис.1.16. Волна частично проходит через границу, а частично отражается от нее. В отличие от анализа задачи с электромагнитными волнами для упругих волн необходимо принять во внимание не три, а пять волн: падающую, поперечную и продольную отраженные и поперечную и продольную преломленные. Если одна из сред является жидкостью или газом, поперечные волны в ней отсутствуют и общее число волн сокращается.
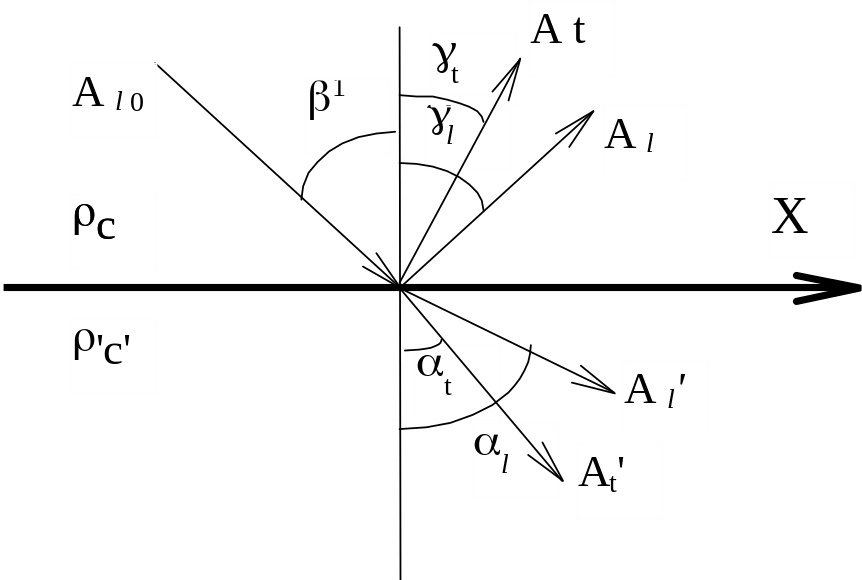
Рисунок 1.16 – Отражение и преломление волн на границе двух твердых сред.
В случае продольной падающей волны выполнение граничных условий эквивалентно следующему:
(1.44)
где cl1, cl2, ct1, ct2 - скорости распространения продольных и поперечных волн в верхней и нижней средах . Отсюда вытекает
(1.45)
Первое из этих соотношений есть закон равенства углов падения и отражения, а остальные являются обобщением закона Снеллиуса на случай упругих волн. Если падающая волна является поперечной, то условия на углы находятся аналогичным образом.
Дальнейшее решение задачи сводится к нахождению амплитуд отраженных и преломленных волн и коэффициентов отражения и прохождения.
Коэффициенты отражения R и прохождения D равны отношениям амплитуд соответствующих отраженных и прошедших и падающих волн, т.е.
(1.46)
где A0 - амплитуда падающей волны.
Коэффициент прохождения (отражения) по энергии выражается соотношением
(1.47)
где
-
коэффициент прохождения для поперечной
волны при падении продольной; Il
и
- интенсивности падающей и преломленной
волн.
Коэффициенты отражения и прохождения по амплитуде
На практике чаще используются коэффициенты по энергии
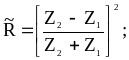
При наклонном падении продольной волны на границу
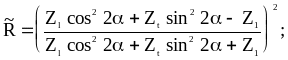
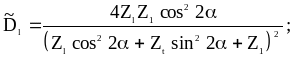
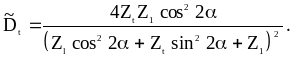
Коэффициент прохождения (отражения) по энергии определяется произведением соответствующих коэффициентов прохождения (отражения) по амплитуде в прямом и обратном направлениях через границу. Например
(1.48)
где
Dlt
-
коэффициент прохождения по амплитуде
для падающей продольной и преломленной
поперечной волн;
- коэффициент прохождения по амплитуде
для падающей поперечной и преломленной
в верхнюю среду продольной волн,
проходящих через границу в обратном
направлении.
Данное соотношение весьма важно для дефектоскопии, в связи с тем, что один и тот же преобразователь, как правило, используется для изучения и приема акустических волн.
Сумма всех коэффициентов отражения и прохождения по энергии равна единице из закона сохранения энергии. Например, при падении продольной волны на границу двух твердых тел
(1.49)
В случае, когда скорость распространения падающей волны меньше, чем скорость распространения какой-либо преломленной (или отраженной) волны, то существует критическое значение угла падения, при котором соответствующая преломленная (или отраженная) волна превращается в неоднородную волну, т.е. концентрируется вблизи границы и быстро затухает при увеличении расстояния.
Рассмотрим условия существования критических углов. Если первой и второй средой являются твердые тела, то из закона синусов вытекает возможность существования целого ряда критических углов.
Первый критический угол I при падении продольной волны существует при условии cl1<cl2. Он соответствует условию слияния продольной преломленной волны с поверхностью
(1.50)
Распространяющаяся вдоль границы неоднородная волна, называемая головной, используется в дефектоскопии. Максимальное значение напряжения головная волна имеет под поверхностью объекта и с ее помощью удается обнаруживать подповерхностные дефекты.
Второй критический угол II существует при условии cl1<ct2 (падает продольная волна) и он соответствует условию слияния с поверхностью преломленной поперечной волны, т.е.
(1.51)
В этом случае неоднородная волна подобна поверхностной рэлеевской волне и их трудно отличить друг от друга.
Третьим критическим углом называют угол падения поперечной волны, про котором отраженная продольная волна превращается в неоднородную. Он определяется выражением
(1.52)
при условии ct2<cl2.
Рассмотрим пример падения продольной волны на границу двух твердых тел, разделенных тонким слоем жидкости: оргстекло - масло - сталь. На границу падает продольная волна, скорость которой cl1<ct2, поэтому имеются два критических угла (cl1=2670 м/с;ct2=3200 м/с). При этих углах все коэффициенты прохождения и коэффициент отражения Rlt обращаются в ноль, а коэффициент отражения Rll=1. В физическом смысле это означает смещение энергии вдоль поверхности неоднородной волной. На рис.1.18 приведены кривые изменения коэффициента прохождения в зависимости от угла падения продольной волны при различной толщине слоя жидкости.
В области углов (10...I) существуют одновременно волны двух типов. В связи с этим существенно затрудняется расшифровка результатов контроля, и поэтому данная область углов используется в дефектоскопии редко.
При первом критическом угле интенсивно возбуждается головная волна, которая применяется при НК.
В интервале между первым и вторым критическими углами существует только поперечная волна. Эта область углов (30...55) широко используется для возбуждения поперечных волн в дефектоскопии.
Аналогичный способ применяют для возбуждения поверхностных волн, волн в пластинах и стержнях. В этом случае угол преломления принимают равным 90, поэтому волны в ограниченных средах возбуждаются при угле падения
(1.53)
где cп - скорость распространения поверхностной волны или фазовая скорость соответствующей моды волны в пластине или стержне.
В практике достаточно трудно получить плоскую волну, для которой выполняются приведенные выше графики и формулы. Вместо этого используют сферические волны, расходящиеся в пределах некоторого угла. При этом значения коэффициентов отражения и прохождения усредняют в некотором интервале углов падения.
Рисунок 1.19 – Отражение и преломление сферической волны на границе двух жидкостей.
При падении на поверхность раздела сред сферической волны отражение и преломление происходят так, как будто каждый из лучей является ограниченной плоской волной. При падении волны с углами несколько большими критического происходит интересное явление - незеркальное отражение. Установлено, что в этом случае отраженный пучок как бы смещается вдоль поверхности тела относительно падающего. Схематически это выглядит следующим образом (рисунок 1.19). При этом, чем ближе значение угла падения к критическому, тем больше смещение . Величина смещения определяется из выражения =2htg, где h - расстояние от действительной поверхности до мнимой границы отражения.
Данное явление можно рассматривать как перенос энергии вдоль поверхности неоднородной волной. Чем ближе угол падения к критическому, тем больше амплитуда неоднородной волны и тем большее расстояние она пробегает вдоль поверхности.