21. Физические основы эхо-метода контроля. Электроакустический тракт дефектоскопа.

Импульсный эхо-метод является в настоящее время наиболее распространенным методом ультразвуковой дефектоскопии, применяемым для контроля различных изделий, в том числе крупногабаритных и сложной формы. Эхо-метод позволяет обнаружить неоднородности в изделии, определить их координаты, размеры и характер путем излучения импульсов УЗ-колебаний, приема и регистрации отраженных от неоднородностей эхо-сигналов.

К преимуществам эхо-метода относятся: односторонний доступ к изделию, относительно большая чувствительность к внутренним дефектам, высокая точность определения координат дефектов. К недостаткам следует отнести: низкую помехоустойчивость к поверхностным отражателям, резкую зависимость эхо-сигнала от ориентации дефекта.

Отличительной особенностью метода является то, что при контроле изделий регистрируются и анализируются практически все сигналы, приходящие из изделия после зондирующих колебаний. Поэтому при контроле изделий с плоскопараллельными поверхностями возможен одновременный прием эхо-сигналов как от дефектов, так и от противоположной поверхности. Причем временное положение эхо-сигнала от дефекта относительно зондирующего импульса пропорционально глубине h его залегания t = 2h/c.

Амплитуда эхо-импульса сложным образом зависит от величины отражателя (дефекта), свойств его поверхности и ориентации, а также затухания ультразвуковых волн в изделии и расстояния до дефекта.

Акустический тракт эхо-дефектоскопа:

Реальные дефекты могут иметь самую разнообразную форму, ориентацию и акустические свойства, которые заранее неизвестны, поэтому формулы акустического тракта выводятся обычно для моделей дефектов в виде полых отражателей простой формы: бесконечно тонкого диска, сферы, цилиндра, бесконечно тонкой полосы, плоскости и т.д. Трудность практического исполнения подобных отражателей вынуждает заменять их искусственными отражателями, например: диск - плоскодонным отверстием, сферу - отверстием со сферическим дном, цилиндр - отверстием с цилиндрическим дном и т.д. При этом амплитуды эхо-сигналов от моделей дефектов и искусственных отражателей мало отличаются, когда их размеры больше длины волны ультразвука. Основные виды искусственных отражателей приведены на рисунке 2.1.

Акустическим трактом называют путь ультразвука от излучателя до объекта, отражающего или рассеивающего ультразвук, и затем к приемнику колебаний. Формулы акустического тракта определяют ослабление амплитуды сигнала на этом пути. Ослабление амплитуды Р эхо-сигнала обычно рассчитывают относительно некоторого максимального значения Р₀, достигаемого при возвращении всей излученной энергии.

Рисунок 2.1 – Искусственные отражатели

При выводе формул акустического тракта не учитывается затухание ультразвука.

22. Основные типы искусственных дефектов. Расчет акустического тракта. Ард-диаграммы и их применение.

Отражение от диска или отверстия с плоским дном. В данном случае можно представить каждую точку В диска, совпадающего с плоским дном отверстия, вторичным источником ультразвука с амплитудой, равной амплитуде падающей волны, умноженной на коэффициент отражения R. При этом будем считать, что точки плоскости вне диска не излучают ультразвук. Тогда выражение для давления на приемнике будет иметь вид

(2.1)

где S_a - площадь преобразователя;

S_b - площадь дна отверстия.

Для границы с воздухом R-1.

В случае небольших размеров дефекта, но превосходящих длину волны , функцию I² на дефекте можно считать постоянной, тогда

(2.2)

где A_д=S_b/² - коэффициент формы дефекта.

В ближней зоне преобразователя I² меняется от 1 до 4, поэтому

(2.3)

а в дальней зоне на оси преобразователя I=S_a/r, тогда

. (2.4)

Видно, что амплитуда отраженной волны от небольшого плоского дефекта не зависит от его формы и пропорциональна его площади. Следует отметить, что если размер дефекта меньше , то описанное выше приближение (Кирхгофа) оказывается неверным, т.е. в этом случае амплитуда отражения убывает с уменьшением отношения b/ (b - радиус отражателя) намного быстрее, чем при b. Является неверным суждение о том, что дефекты размером меньше длины волны не выявляются, т.к. в этом случае отражение имеется, но уменьшается оно гораздо существеннее.

Когда площадь отражателя приближается к площади преобразователя, то нельзя считать функцию I на поверхности дефекта постоянной. Поскольку I уменьшается от центра к периферии, амплитуда сигнала возрастает с ростом дефекта медленнее, чем по закону S_b/².

Если размеры отражателя превосходят размеры преобразователя, необходимо учитывать при оценке эхосигналов в какой зоне находится отражатель (ближней или дальней), а также тот факт, что и отражатель, являясь вторичным излучателем, имеет ближнюю и дальнюю зоны, в которые попадает приемник.

Как видно из выражения (2.1) величину P/P₀ можно представить как функцию двух безразмерных параметров: отношения диаметра диска к диаметру преобразователя (2b/2a) и отношения расстояния от преобразователя до отражателя к длине ближней зоны преобразователя (r/r_б). На основе этого ослабление амплитуды сигнала в широком диапазоне диаметров плоского отражателя и расстояний до него находят по безразмерной диаграмме амплитуда - расстояние - диаметр (рисунок 2.2), так называемой АРД-диаграмме. По ней определяют максимальную амплитуду эхосигнала от диска, расположенного на данной глубине. Затухание ультразвука в данной диаграмме не учтено. По безразмерной АРД-диаграмме строят размерные диаграммы для конкретных типов преобразователей. Здесь все параметры выражаются в прямых единицах. Для учета затухания ультразвука размерные диаграммы вставляют в планшет, имеющий поворотную сетку линий. Сетку поворачивают относительно оси абсцисс на угол, определяемый коэффициентом затухания , и линиями сетки пользуются вместо горизонтальных линий координат АРД-диаграммы.

АРД-диаграммы применяют для настройки чувствительности перед контролем и для определения эквивалентных размеров дефектов. Эта величина определяется как диаметр или площадь плоскодонного отражателя, расположенного на той же глубине, что и реальный дефект, и дающего одинаковую с дефектом амплитуду эхо-сигнала.

Отражение от цилиндра. Ослабление амплитуды эхо-сигнала от бесконечного протяженного цилиндра в дальней зоне преобразователя определяют из выражения

(2.5)

где d - диаметр цилиндра.

Однако это выражение используется, когда d и r соизмеримы. Если диаметр отражающего цилиндра значительно меньше расстояния r до него (как в эталонах), формула имеет вид

(2.6)

где - коэффициент формы цилиндрического отражателя.

При контроле применяют эталонные образцы (СО3) в форме полуцилиндра, в центральной части которого располагают преобразователь. В этом случае в плоскости, перпендикулярной оси цилиндра, излученная энергия полностью (без учета затухания) возвращается обратно к преобразователю, а в плоскости оси цилиндра энергия расходится, как при отражении от бесконечной плоскости. Тогда в дальней зоне получаем

(2.7)

Данные образцы используют для определения акустического центра преобразователя и для оценки максимальной амплитуды эхо-сигнала. Для цилиндрических отражателей строятся также размерные АРД-диаграммы.

Все приведенные выше формулы не учитывают затухания ультразвука в акустическом тракте.

Рассмотрим некоторые формулы для расчета амплитуд акустических эхо-сигналов от моделей дефектов с учетом затухания при контроле с дисковым преобразователем.

Для диска (отверстие с плоским дном) диаметром 2b: при r+r₁<r_б

(2.8)

при r+r₁>3r_б

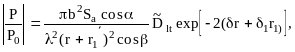(2.9)

где  - длина волны в изделии;

r - путь ультразвука в изделии;

r₁ - средний путь в призме преобразователя;

r₁- путь ультразвука от мнимой пьезопластины до точки ввода в изделие;

D_lt - коэффициент прохождения через границу призма-изделие;

 и ₁ - затухание ультразвука в изделии и призме;

 - угол наклона призмы.

Для бесконечного цилиндра диаметром 2b: при r+r₁>3r_б

(2.10)

при r+r₁<r_б

(2.11)

где а - радиус пьезопластины.

Для бесконечной плоскости: при r+r₁<r_б

(2.12)

при r+r₁>3r_б

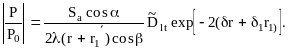(2.13)

Для сферы (отверстие со сферическим дном) диаметром 2b: при r+r₁<r_б

(2.14)

при r+r₁>3r_б

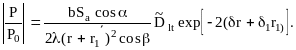(2.15)

В связи со сложностью изготовления отверстий с плоским дном, ориентированных строго перпендикулярно акустической оси преобразователя, при контроле наклонным преобразователем допускается применение сегментных и угловых отражателей. Для того, чтобы амплитуда эхо-сигнала от сегментного отражателя была равна амплитуде от плоскодонного отверстия такой же площади, высота сегментного отражателя должна быть больше длины поперечной волны, а отношение высоты h к ширине b не менее 0,4. Ширина b и высота h углового отражателя должны быть больше длины поперечных волн. т.е. 4>h/b>0,5.

В практике контроля следует учитывать, что реальные дефекты отличаются от рассмотренных моделей неправильностью формы и шероховатостью поверхности. Они могут быть пустыми или заполненными инородными веществами. Все это оказывает влияние на ослабление амплитуды эхо-сигналов. Так, например, шероховатость поверхности отражателя ослабляет амплитуду сигнала, когда величина неровностей превосходит /3. Шлаки и другие вещества, заполняющие дефект, снижают амплитуду отраженного сигнала приблизительно пропорционально коэффициенту отражения. Если акустические характеристики основного материала и неоднородностей сравнимы, то наблюдается резкое уменьшение амплитуды эхо-сигнала.