Глава 23

,или кортежей оценок

либо группой це­

где

левых функций (функций ценности, полезности)

— индивидуальная оценка варианта по кри­терию K_q, данная участником Основываясь на

ГРУППОВОЙ МНОГОКРИТЕРИАЛЬНЫЙ ВЫБОР

23.1. Многокритериальный подход к коллективному выбору

Многоаспектный анализ сложной, плохо формализованной проблемы обычно выполняется группой специально отобран­ных высококвалифицированных экспертов, которые выполняют функции членов ГПР. Эксперты анализируют возможные пути решения проблемы, формируют перечень альтернативных вари- антов, дают свои независимые субъективные оценки вариантов по многим критериям. Эти оценки обрабатываются каким-либо Методом, и ищется один лучший или несколько приемлемых ва­риантов решения. Полученные результаты обсуждаются всеми экспертами и могут быть дополнены и изменены с целью их улучшения.

В решении проблемы, как правило, принимает также уча­стие руководитель более высокого ранга, который несет общую Ответственность за ее решение. Такой руководитель называет­ся суперЛПР. СуперЛПР определяет критерии оценки вариан­тов, рассматривает полученные от экспертов индивидуальные заключения и результаты предварительного анализа проблемы, делает окончательный выбор. Обычно суперЛПР отвечает и за подбор экспертов.

Задача коллективного многокритериального выбора состоит В следующем. Имеется т вариантов решения проблемы

которые оценены независимо t членами ГПР или экспер­тами по п критериям Каждый критерий имеет свою собственную шкалу оценок — непрерывную или дис­кретную, числовую или вербальную. Порядковые шкалы оце­нок обычно предполагаются упорядоченными, например, от наи- |5олее предпочтительных значений к наименее предпочтитель­ным. Вариант представляется группой n-мерных векторов

предпочтениях суперЛПР и/или учитывая экспертные оценки членов ГПР, требуется решить одну из следующих задач: 1) вы­делить один или несколько лучших вариантов; 2) упорядочить все варианты от лучшего к худшему; 3) распределить все вари­анты по классам решений.

Реальный процесс принятия решения зачастую не является одноразовой процедурой. Нередко выполняется несколько по­вторяющихся туров, в которых варианты, критерии, эксперты появляются, заменяются, исключаются до тех пор, пока не бу­дет найдено приемлемое решение.

Коллективный многокритериальный выбор имеет ряд специ­фических особенностей. Эксперты, как члены ГПР, в общем слу­чае могут быть неравноправными. Различная степень компетен­ции и/или влиятельности экспертов учитывается при агрегиро­вании индивидуальных предпочтений. Допускается также, что разные критерии могут иметь, вообще говоря, различную инди­видуальную важность (вес) для суперЛПР и для каждого участ­ника. Важность критерия можно задать, воспользовавшись од­ним из способов, указанным в разд. 8.3.

При нахождении итогового агрегированного результата неред­ко используется формальная аналогия между множественностью индивидуальных предпочтений членов ГПР и множественностью критериев оценки вариантов. Сначала для каждого члена ГПР решается своя задача индивидуального многокритериального вы­бора. Полученные результаты решения t индивидуальных задач принимаются в качестве исходных при решении новой задачи группового многокритериального выбора, где члены ГПР высту­пают в роли новых критериев. В этом случае показатель компе­тентности и/или влиятельности участника выступает аналогом относительной важности критерия. Подобный подход применя­ется, например, в теории многомерной полезности.

Итоговый выбор, очевидно, не должен зависеть от очеред­ности выполнения процедур обработки индивидуальных много­критериальных оценок (сначала по членам ГПР, а потом по кри­териям, или наоборот). Это условие независимости результата от очередности учета предпочтений индивидуумов или оценок по критериям представляется естественным «разумным» требо­ванием рациональности коллективного выбора и может быть на­звано принципом инвариантности агрегирования индивидуаль­ных многокритериальных предпочтений.

Одним из важных аспектов, на который необходимо обра­щать внимание при обработке и анализе информации в задачах

коллективного многокритериального выбора, является пробле­ма сопоставимости разнородных данных. Шкалы количествен­ных критериев оценок имеют обычно разную размерность. На­пример, стоимость, длина, время, скорость измеряются соответ­ственно в рублях, метрах, секундах, километрах в час. Как пра­вило, именованные показатели приводят к безразмерным, а ча­сто их еще и нормируют, используя один из способов, упомяну­тых в разд. 3.5.

Качественные критерии оценок имеют различное содержание и разнообразные шкалы. Для унификации качественных шкал можно использовать лингвистические переменные вида: «отлич­но», «хорошо», «удовлетворительно», «плохо», «неудовлетвори­тельно». Во многих методах применяется оцифровка лингвисти­ческих переменных, например с помощью балльных шкал. Одна­ко такая квантификация качественных шкал может приводить к существенным искажениям индивидуальных предпочтений чле­нов ГПР, а значит, оказывает влияние на результаты коллектив­ного выбора.

Кроме того, следует учитывать «разнонаправленность» кри­териев, которая выражает разное качество решения. «Положи­тельные» критерии, по которым большие значения оценок счи­таются предпочтительными (лучшими), обычно ассоциируются с «доходами». «Отрицательные» критерии, для которых пред­почтительными будут меньшие значения оценок, уподобляют «расходам». Такая ситуация уже встречалась в задачах мно­гокритериальной оптимизации, где оценки по одним целевым функциям нужно было максимизировать, а по другим — мини­мизировать.

23.2. Оценка компетентности экспертов

Привлечение нескольких экспертов к поиску решения про­блемы порождает необходимость учета их индивидуальных ин­тересов и мнений, которые не всегда могут быть одинаково зна­чимы для суперЛПР. Компетентность эксперта как специалиста характеризуют его профессиональные знания и опыт, аналитич­ность и широта мышления, уровень квалификации в определен­ной области.

Компетентность эксперта можно оценить, вообще говоря, лишь опираясь на мнения других лиц или на результаты про­шлой деятельности эксперта. Пусть список экспертов формиру-

ется путем опроса специалистов. По результатам опроса состав­ляется матрица в которой если эксперт р предложил включить эксперта s в группу, и "в противо­положном случае. Тогда показатель компетентности к^ экспер­та s можно определить как число поданных за него голосов:

(23.1)

Вместе с тем такой упрощенный подход к оценке компетент­ности не позволяет учесть всю многогранность и сложность этой характеристики эксперта.

Для вычисления показателя компетентности эксперта JI. Г. Евланов и В.А.Кутузов (СССР, 1978) предложили эври­стическую итеративную процедуру, которая базируется на ин­дивидуальных оценках , данных экспертом s i-му варианту

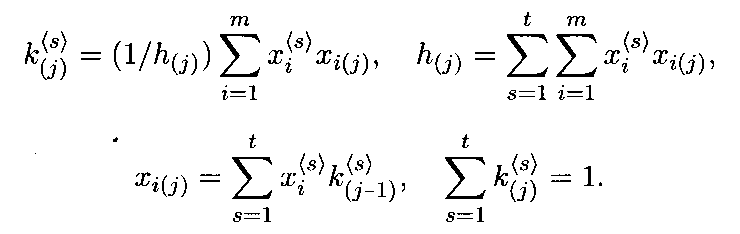
1. Первоначально показатели компетентности всех экспертов полагаются равными

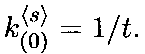
2. На каждом последующем шаге показатель компетентности каждого эксперта s корректируется по формуле средней оценки

3. Процедура продолжается до получения приемлемого ре­зультата.

Таким образом, компетентность экспертов оценивается по степени согласованности их индивидуальных оценок с группо­вой экспертной оценкой. Однако данная процедура не всегда да­ет удовлетворительные результаты, а ее сходимость строго не обоснована.

й

Обычно принято считать экспертов достаточно точными ге­нераторами и измерителями информации. В таком случае мож­но ожидать, что достоверность получаемой экспертной инфор­мации будет повышаться при увеличении числа экспертов. Вме­сте с тем возрастают временные и финансовые затраты на прове­дение экспертизы. Поэтому общее число экспертов должно опре-

делиться разумным компромиссом между степенью достоверно­сти экспертных суждений и допустимой величиной расходов на экспертизу.

Для оценки достоверности суждений эксперта используется показатель — число случаев, в кото­

рых суждения эксперта s получили практическое подтвержде­ние; М — общее число случаев участия эксперта в эксперти­зе. Тогда средняя достоверность суждений группы экспертов

а относительная достоверность суждений

эксперта s в группе

Однако применение таких показателей достоверности экс­пертных суждений требует надежной статистической информа­ции о результатах практического участия многих экспертов в различных экспертизах. А подобная информация, как правило, либо отсутствует, либо труднодоступна.