
- •Часть IV
- •Глава 20
- •20.4. Классификация задач и методов коллективного выбора
- •Глава 21 голосование
- •21.9. Свойства процедур голосования
- •Свойства процедур голосования
- •Глава 22
- •22.7. Условия рациональности выбора в функциональной модели
- •Глава 23
- •23.1. Многокритериальный подход к коллективному выбору
- •23.3. Статистический анализ экспертных суждений
- •7. Для каждого варианта задается показатель его удаленности от наихудшего опорного варианта как
- •23.11. Особенности групповых
- •23.12. Общая характеристика методов коллективного выбора
- •Глава 21 голосование 299
- •Глава 22 313
- •Глава 23 340
Глава 21 голосование
21.1. Механизмы и процедуры голосования
Голосование — один из наиболее распространенных, популярных и давно известных способов коллективного принятия решений, который применяется для выбора наиболее предпочтительного для всех варианта в различных по размеру группах. Если число избирателей достаточно велико, то такой выбор называют социальным или общественным.
Разные системы голосования отличаются используемыми процедурами сравнения вариантов, правилами подсчета голосов и определения победителей, формами организации и проведения выборов. «Честные» выборы предполагают независимость избирателей, свободу волеизъявления голосующих, отсутствие нарушений установленных процедур и правил голосования. Вместе с тем, как оказалось, разные системы голосования могут давать различные результаты даже при соблюдении всех условий «честности» выборов.
Обоснование процедур голосования и формализация правил подсчета голосов для определения победителей были одними из первых задач коллективного принятия решений, привлекших внимание исследователей. Еще в конце XVIII в. французские ученые Жан Борда, математик, физик и морской штурман, и маркиз Жан де Кондорсё, общественный деятель, секретарь Французской академии, философ-просветитель, математик и социолог, приступили к систематическому изучению задачи голосования. Борда доложил свои результаты по формам выборов на заседании Королевской академии наук в Париже в 1770 г. и опубликовал их в 1784 г., а Кондорсе — в 1785 г. В XIX в. проблемы голосования изучались французским математиком и физиком П. Лапласом и английским математиком Ч. Доджсоном. Первым же, кто предложил (1951) аксиоматику рационального коллективного выбора, был К. Эрроу, американский математик и экономист, впоследствии лауреат Нобелевской премии.
Голосование объединяет два механизма: индивидуальный выбор избирателей и подведение итогов выборов, которые обычно выполняются разными людьми. Индивидуальный выбор осу-
ществляется всеми избирателями, которыми могут быть жители страны, области или города, члены комитета или жюри. Очевидно, механизмы голосования и волеизъявления должны быть простыми и понятными для всех избирателей. Для выявления индивидуальных предпочтений избирателей применяются две основные разновидности процедур: неранжирующая и ранжирующая.
В неранжирующей процедуре голосования каждый избиратель отдает свой голос за один или несколько имеющихся альтернативных вариантов. В одних процедурах следует голосовать только за определенное число вариантов, например за одного кандидата на парламентских выборах или за нескольких претендентов по числу лиц, избираемых в состав руководящего органа; в других допускается голосование за любое произвольное число вариантов. Голоса, поданные за каждый вариант, суммируются.
В ранжирующих процедурах голосования требуется, чтобы каждый избиратель оценивал все имеющиеся варианты. В одних случаях предлагается полностью или частично упорядочить все варианты по предпочтительности и расположить их в порядке убывания предпочтительности; в других необходимо провести парное сравнение вариантов и указать предпочтительность одного из них.
Результаты голосования подводит независимая избирательная комиссия по определенным правилам и под строжайшим наблюдением и контролем. Механизм подсчета голосов может быть и не очень простым по сравнению с механизмом голосования, но он должен быть прозрачным, точным и эффективным.
При подсчете голосов учитывается ряд дополнительных условий. Если все избиратели являются равноправными участниками, то обычно один голосующий имеет 1 голос или т голосов по числу сравниваемых вариантов при так называемом кумулятивном голосовании. В последнем случае голосующий должен по своему усмотрению распределить эти т голосов между произвольными вариантами. Если избиратели неравноправны, то каждый из них располагает определенным и, как правило, неравнозначным числом голосов. Например, председатель жюри или генеральный директор компании имеет право на два голоса при рассмотрении спорных ситуаций; акционер имеет число голосов, равное количеству принадлежащих ему акций; выборщики на выборах президента США имеют число голосов, равное числу избирателей штата, и все эти голоса отдаются одному кандидату, победившему в штате на промежуточных выборах.
21.2. Правила определения победителя
Для определения лучшего по итогам голосования варианта наиболее часто используются следующие правила:
один голос «за» или 1-большинство голосов — лучшим считается вариант, за который проголосовал хотя бы один участник, а остальные участники воздержались от выбора;
относительное большинство голосов — лучшим считается вариант, за который проголосовало большинство участников (больше, чем за любой другой вариант, но необязательно более половины от общего числа голосов);
простое большинство голосов — лучшим считается вариант, за который проголосовало простое большинство участников (более половины от общего числа голосов);
абсолютное или квалифицированное большинство голосов — лучшим считается вариант, за который проголосовало больше заранее заданного числа участников (например, более двух третей или более трех четвертей от общего числа голосов);
(к1,к2)-большинство голосов — лучшим считается вариант, за который проголосовало не менее чем к1 участников и против — не более чем к2 участников;
единогласие — лучшим считается вариант, за который проголосовали все участники;
вето — вариант не выбирается, если против него проголосовал хотя бы один участник независимо от результатов голосования остальных участников.
Каждому из правил большинства голосов можно сопоставить некоторое мажоритарное отношение, по которому определяется победитель при попарном сравнении вариантов, аналогичное приведенному в разд. 19.5. Все правила большинства голосов можно объединить одним правилом к- большинства, где число к устанавливает порог большинства голосов или так называемую квоту. Участники, проголосовавшие одинаково, представляют собой коалицию.
В применяемых на практике системах голосования используются разные виды итогового коллективного выбора. В качестве основных результатов выбора укажем: выбор единственного варианта из имеющихся; выбор заданного числа вариантов; выбор произвольного числа вариантов; упорядочение всех или определенной части вариантов. Так, в системе мягкого рейтинга каждый участник может голосовать за любое произвольное число имеющихся вариантов. Победитель определяется по правилу от-
носительного большинства голосов. Такая система голосования часто используется в парламентах.
Системы голосования различаются также формами своей организации (одно-, многотуровые), правилами определения победителей каждого тура. В многотуровых процедурах коллективного принятия решений процесс поиска победителя или итогового упорядочения вариантов разбивается на несколько туров или этапов, на каждом из которых может использоваться своя система голосования, свои правила подсчета голосов и определения победителей, выходящих в следующий тур выборов. Например, в системе голосования, основанной на процедуре исключения худшего варианта, каждый участник попарно сравнивает все варианты по предпочтительности. Вариант, признанный худшим большинством голосов участников, исключается из рассмотрения. Процедура повторяется до тех пор, пока не останется единственный лучший вариант. Эта система голосования используется в конгрессе США.
Победители конкурсов определяются коллективным решением жюри, которое обычно также принимается голосованием. Если конкурс проводится в несколько туров и по разным группам участников (например, в музыкальном конкурсе принимают участие пианисты, скрипачи, виолончелисты и другие музыканты), то вначале специализированные по номинациям жюри проводят последовательный отсев участников, допуская к следующему туру только часть лучших исполнителей. На заключительном туре определяются победители по каждому виду конкурса, занявшие первое, второе и третье места. На окончательное распределение мест могут повлиять оценки, полученные участниками на каждом из туров, а также состав участников. Часто фавориты получают завышенные оценки независимо от показанных результатов. Кроме того, на каждом отдельном туре и по каждому виду конкурса могут использоваться свои процедуры и правила для определения лучших участников и победителей, что тоже оказывает свое влияние на итоговые результаты конкурса.
Для оценки применимости той или иной системы голосования весьма существенно установить, какие правила необходимы и достаточны в реальных условиях, чтобы адекватно упорядочить кандидатов и/или определить победителя. Оказалось, что использование того или иного способа обработки и подсчета поданных голосов может заметно повлиять на итоговые результаты голосования и дать разных победителей выборов. Такие ситуации получили название парадоксов голосования. Первый па-
радокс голосования был обнаружен де Кондорсе (1785) и впоследствии получил его имя. Позднее были найдены и другие парадоксы коллективного выбора.
Рассмотрим наиболее известные процедуры голосования.
21.3. Процедуры Борда
Процедура Борда (1770) была исторически первой системой голосования, где использовалась ранжирующая процедура учета мнений голосующих. Она является естественным и корректным способом коллективного выбора, который обеспечивает всем участникам возможность выразить индивидуальные предпочтения и позволяет учесть интересы меньшинства. Процедура состоит из следующих шагов.
Каждый участник ранжирует все варианты
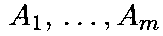 по
предпочтительности.
по
предпочтительности.В каждом 5-м индивидуальном строгом упорядочении первый вариант получает m — 1 баллов, второй вариант — m — 2 баллов, последний вариант — 0 баллов. Очевидно, что в s-м упорядочении балл Борда
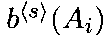 каждого
варианта
каждого
варианта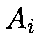 равен
числу
равен
числу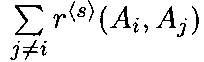 вариантов
вариантов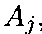 ,
которые уступают варианту
,
которые уступают варианту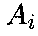
Здесь
величина![]() ,
если
,
если![]() ,
и
,
и![]() ,
,
если![]()
Для каждого варианта
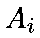 вычисляется
значение функции Борда
вычисляется
значение функции Борда
![]()
равное
сумме баллов Борда![]() ,
присвоенных варианту
,
присвоенных варианту![]() во
во
всех индивидуальных упорядочениях.
Упорядочение вариантов строится поубыванию значения функции Борда
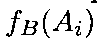 .
Лучший вариант
.
Лучший вариант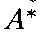 определяется
максимальным значением функции
Борда
определяется
максимальным значением функции
Борда
![]()
Отметим,
что балл Борда![]() связан
с рангом
связан
с рангом![]() ва
ва
рианта![]() ,
введенным формулой (3.1), соотношением:
,
введенным формулой (3.1), соотношением:![]()
![]() Тем
самым убывающая последовательность
баллов
Тем
самым убывающая последовательность
баллов
Борда![]() эквивалентна
возрастающей по
эквивалентна
возрастающей по
следовательности
рангов вариантов![]()
Пример 21.1I. Предположим, что 60 избирателей должны выбрать одного из трех кандидатов А, В и С. Пусть при использовании ранжирующей процедуры учета мнения избирателей их индивидуальные предпочтения распределились следующим образом:
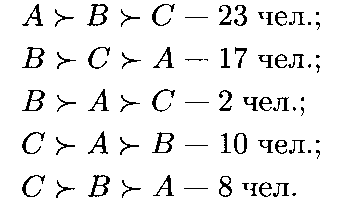
Вычислим
значение функции Борда![]() для
каждого из кандидатов, полагая, что
в индивидуальном упорядочении первому
кандидату присваивается 2 балла, второму
— 1 балл, третьему — 0 баллов.
для
каждого из кандидатов, полагая, что
в индивидуальном упорядочении первому
кандидату присваивается 2 балла, второму
— 1 балл, третьему — 0 баллов.
Тогда получаем:
для кандидата А
![]()
для кандидата В
![]()
для кандидата С
![]()
Упорядочение
кандидатов в соответствии со значениями
функции Борда![]() имеет
вид:
имеет
вид:![]() поскольку
поскольку
![]() .
Лучшим является кандидат В. ■
.
Лучшим является кандидат В. ■
Модифицированная процедура Борда учитывает возможные различия индивидуальных предпочтений избирателей.
Каждый участник ранжирует все варианты
 по
предпочтительности.
по
предпочтительности.Подсчитывается количество индивидуальных строгих упорядочений одного и того же вида.
Для каждого варианта
 подсчитывается
общее число
подсчитывается
общее число
![]() участников,
предпочитающих данный вариант
участников,
предпочитающих данный вариант![]() всем
остальным вариантам
всем
остальным вариантам
![]() при парных сравнениях во всех полученных
упорядочениях.
при парных сравнениях во всех полученных
упорядочениях.
Для каждого варианта
 вычисляется
значение модифицированной функции
Борда
вычисляется
значение модифицированной функции
Борда
![]()
Упорядочение вариантов строится по убыванию значения модифицированной функции Борда
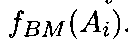 .
Лучший вариант
.
Лучший вариант
![]() определяется
максимальным значением функции Борда
определяется
максимальным значением функции Борда
![]()
Вместо шагов 1, 2 каждый голосующий может попарно сравнить все варианты друг' с другом и по результатам сравнений построить упорядочение вариантов (см. разд. 4.1).
Нетрудно
убедиться, чтофункция Борда![]() представ
представ
ляет
собой общее число![]() участников,
предпочитающих
участников,
предпочитающих
данный
вариант![]() всем
остальным вариантам
всем
остальным вариантам![]() при
при
парных сравнениях:
![]()
Пример
21.2.
Пусть выполняются условия примера 21.1.
Вычислим значения функций Борда для
каждого из кандидатов .![]() Если
во всех упорядочениях рассматривать
только парные сравнения кандидатов
Если
во всех упорядочениях рассматривать
только парные сравнения кандидатов![]() 1
избирателя считают кандидата
А
предпочтительнее кандидата
1
избирателя считают кандидата
А
предпочтительнее кандидата
![]() избирателей
— кандидата
В предпочтительнее
кандидата
А.
Аналогичным образом, сравнивая
остальные пары кандидатов, получим
избирателей
— кандидата
В предпочтительнее
кандидата
А.
Аналогичным образом, сравнивая
остальные пары кандидатов, получим
![]()
Значения
функции Борда![]() для
кандидатов:
для
кандидатов:
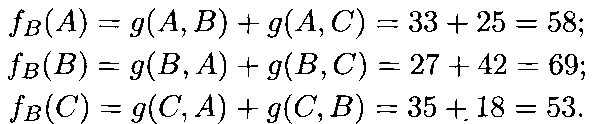
Таблица 21.1
Групповая
матрица G
парных
сравнений, функции Борда
кандидатов
G
А
В
С
fв
fвm
А
—
33
25
58
-4
В
27
—
42
69
18
С
35
18
—
53
-14
![]()
Значения
модифицированной функции Борда![]()

Представим
распределение числа избирателей при
парных сравнениях кандидатов .![]() групповой
матрицей
групповой
матрицей
![]()
![]() Значения
элементов матрицы G
и
функций Борда указаны в табл. 21.1.
Упорядочение
Значения
элементов матрицы G
и
функций Борда указаны в табл. 21.1.
Упорядочение![]() кандидатов в соответствии со значениями
модифицированной функции Борда
кандидатов в соответствии со значениями
модифицированной функции Борда![]() имеет
вид:
имеет
вид:![]() ,
поскольку
,
поскольку
![]() .
Лучшим является кандидат В. Тот же
результат дает применение функции
Борда
.
Лучшим является кандидат В. Тот же
результат дает применение функции
Борда![]() . ■
. ■
21.4. Процедура Кондорсе
Анализируя различные системы голосования, Кондорсе сформулировал принцип, обеспечивающий, по его мнению, честные и справедливые результаты выборов. Как писал Кондорсе, «существует только один правильный путь выяснения мнения большинства на выборах. Он состоит в попарном сравнении соответствующих достоинств кандидатов... Тот, кто действительно получает предпочтение большинства голосов на выборах, должен казаться наиболее превосходящим своих конкурентов и, таким образом, является тем, кто утверждается боль-
шинством голосов, как превосходящий всех»I. Другими словами, принцип Кондорсе гласит: победителем на выборах объявляется кандидат, превосходящий при попарном сравнении все$ остальных кандидатов по правилу простого большинства голосов. В таком случае нет необходимости проводить многократное баллотирование кандидатов.
Процедура Кондорсе (1785), реализующая этот принцип, базируется на ранжирующей процедуре учета мнений голосующих и состоит из следующих шагов.
1 — 3. Совпадают с шагами 1 — 3 модифицированной процедуры Борда и состоят в построении группового распределения участников, попарно сравнивающих предпочтительность вариантов по отношению друг к другу во всех полученных индивидуальных строгих упорядочениях.
4. Лучший вариант при попарном сравнении вариантов определяется по правилу простого большинства голосов.
Пример 21.3. Пусть выполняются условия примера 21.1 и предпочтения избирателей при попарном сравнении кандидатов А, В и С распределились так:
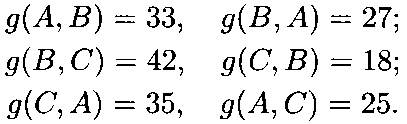
По
мнению большинства избирателей, кандидат
А
превосходит кандидата В,
поскольку![]() Аналогично,
кандидат
В
превосходит кандидата С, так как
Аналогично,
кандидат
В
превосходит кандидата С, так как![]() ,
а кандидат
С
кандидата
А,
так как
,
а кандидат
С
кандидата
А,
так как![]() .
Таким образом, получается несогласованное
коллективное предпочтение:
.
Таким образом, получается несогласованное
коллективное предпочтение:
![]() ,
содержащее цикл, вследствие чего нельзя
выбрать лучшего кандидата. ■
,
содержащее цикл, вследствие чего нельзя
выбрать лучшего кандидата. ■
Причина
возникшего противоречия — так называемого
парадокса Кондорсе
— состоит в том, что результаты парных
сравнений вариантов, полученные
путем суммирования количества
индивидуальных упорядочений, являются
взаимозависимыми. Если индивидуум
утверждает, что![]() ,
то должно быть и
,
то должно быть и
![]() .
Однако когда правило большинства
применяется
.
Однако когда правило большинства
применяется
к совокупности этих индивидуальных утверждений, результаты \могут оказаться другими, в том числе и несогласованными. \ Действительно, в примере 21.3 кандидат А предпочтительнее кандидата В по большинству голосов («за» — 33 голоса), ^предпочтительнее С («за» — 42 голоса), С предпочтительнее Л\(«за» — 35 голосов). Но эти три множества избирателей, голосовавших «за» своего кандидата, совершенно различны. Боле^ того, эти множества даже не пересекаются, поскольку нет ни одного участника, который одновременно входил бы во все три множества голосующих «за».
Если воспользоваться правилом абсолютного большинства, то победителем станет кандидат набравший 42 голоса при парных сравнениях с остальными кандидатами. В то же время согласно правилу относительного большинства при неран- жирующей процедуре учета мнений избирателей лучшим кандидатом должен быть признан кандидат А, за которого высказались 23 голосовавших, тогда как за кандидата В было подано 17 + 2 = 19 голосов, а за кандидата С — 10 + 8 = 18 голосов. Как видно, результаты выборов существенно зависят от принятой системы голосования. Итак, может оказаться, что у группы участников не будет единственного обоснованного коллективного предпочтения.
Заметим также, что в общем случае вариант, лучший по процедуре Кондорсе, может не совпадать с вариантом, лучшим по процедуре Борда.
21.5. Процедуры Симпсона
Процедура Симпсона (1965) позволяет избежать возникновения парадокса несогласованности Кондорсе и состоит в следующем:
1 — 3. Совпадают с шагами 1 — 3 модифицированной процедуры Борда и процедуры Кондорсе.
Для каждого варианта
 определяется
значение функции Симпсона
определяется
значение функции Симпсона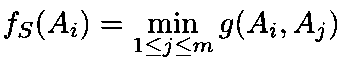
равное
минимальному числу участников,
предпочитающих данный вариант![]() всем
остальным вариантам
всем
остальным вариантам
![]() при
всех парных сравнениях.
при
всех парных сравнениях.
Упорядочение вариантов строится по убыванию значения функции Симпсона
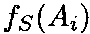 .
Лучший вариант
.
Лучший вариант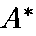 определяет-
определяет-
Таблица
21.2
Групповая
матрица
G
парных
сравнений, функции Симпсона
G
А
В
С
fs
/т
А
33
25
25
33
В
27
42
27
42
С
35
18
—
18
35
![]() кандидатов
кандидатов
ся максимальным значением функции fs или правилом макси- мина:
![]()
В процедуре, двойственной процедуре Симпсона, для определения лучшего варианта А* используется правило минимакса:
![]()
В
этих процедурах правила определения
лучшего варианта А* являются аналогами
правил «гарантированного результата»,
выявляющего победителя группового
турнира, а групповая матрица парных
сравнений кандидатов![]() ,
где
,
где
![]() ,
аналогична турнирной матрице (см. разд.
19.5).
,
аналогична турнирной матрице (см. разд.
19.5).
Пример 21.4' Пусть выполняются условия примера 21.1. Вычислим значения двойственных функций fs и fx для каждого из кандидатов А, В и С:

Групповая матрица парных сравнений кандидатов G = = (9ij)mxm, 9ij = g(Ai,Aj), и значения функций Симпсона fs и fx приведены в табл. 21.2.
Упорядочение
кандидатов в соответствии со значениями
функции fs
имеет
вид:![]() ,
поскольку
,
поскольку![]()
![]() .
Лучшим является кандидат В. Упорядочение
кандидатов в соответствии со значениями
функции
fx
имеет
вид:
.
Лучшим является кандидат В. Упорядочение
кандидатов в соответствии со значениями
функции
fx
имеет
вид:
v![]() поскольку
/т(А) <
fr{C)
<
/т(-В). Лучшим яв
поскольку
/т(А) <
fr{C)
<
/т(-В). Лучшим яв
ляется кандидат А. Таким образом, в общем случае лучшие варианты, выбранные по правилам максимина и минимакса, могут не совпадать друг с другом. ■
21.6. Процедура Доджсона
!Процедура Доджсона (1877) представляет собой модификацию подхода Кондорсе, которая позволяет устранить несогласованность коллективного предпочтения при построении результирующего упорядочения вариантов. Основная идея процедуры Доджсона заключается в следующем: все варианты упорядочиваются по числу голосов, которых им не хватает для того, чтобы превосходить все остальные варианты по простому большинству (более половины от общего числа) голосов.
1 — 3. Совпадают с шагами 1 — 3 модифицированной процедуры Борда и процедуры Кондорсе.
Строится вспомогательная матрица
 ,
где hij
=
,
где hij
=
![]() —
групповая
матрица парных сравнений вариантов по
числу поданных голосов. Для каждого
варианта
—
групповая
матрица парных сравнений вариантов по
числу поданных голосов. Для каждого
варианта
![]() по
строке матрицы Н находятся варианты
по
строке матрицы Н находятся варианты![]() ,
для которых
,
для которых
![]() Это
как раз и будут те варианты, в сравнении
с которыми вариант А{ получил меньше
половины от общего числа голосов.
Обозначим совокупность таких вариантов
через /4i/2-
Это
как раз и будут те варианты, в сравнении
с которыми вариант А{ получил меньше
половины от общего числа голосов.
Обозначим совокупность таких вариантов
через /4i/2-
Для каждого варианта А{ вычисляется значение функции Доджсона
![]()
где![]() если
число
t
избирателей
четно, и
если
число
t
избирателей
четно, и![]()
при нечетном t.
Упорядочение вариантов строится по возрастанию значения функции Доджсона
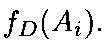 Лучший
вариант А* определяется минимальным
значением функции Доджсона
Лучший
вариант А* определяется минимальным
значением функции Доджсона
![]()
Пример
21.5.
Пусть выполняются условия примера 21.1.
Представим распределение числа голосов
избирателей при попарном сравнении
кандидатов А,
С
двумя групповыми матрицами![]() (табл.
21.3).
(табл.
21.3).
Кандидат А превосходит кандидата Б, а чтобы превосходить кандидата С по простому большинству голосов кандидату А не
Таблица
21.3
Групповые
матрицы
G
и
Н
парных сравнений, функция Доджсона
Н
А
В
С
А
—
33/27
25/35
В
27/33
—
42/18
С
35/25
18/42
—
![]() кандидатов
кандидатов
хватает![]() Аналогично,
кан
Аналогично,
кан
дидату
В
не хватает![]() голосов,
что
голосов,
что
бы
превосходить кандидата
А
по простому большинству голосов, а
кандидату
С
не хватает![]() голосов,
чтобы превосходить кандидата В. Тогда
значения функции Доджсона
голосов,
чтобы превосходить кандидата В. Тогда
значения функции Доджсона![]() для
кандидатов будут равны:
для
кандидатов будут равны:![]()
![]()
Упорядочение
кандидатов в соответствии со значениями
функции Доджсона![]() имеет
вид:
имеет
вид:![]() ,
поскольку
,
поскольку
![]() Лучшим
является кандидат В. Заметим, что в
данном примере для каждого варианта А{
есть только один превосходящий его
вариант
Лучшим
является кандидат В. Заметим, что в
данном примере для каждого варианта А{
есть только один превосходящий его
вариант![]() .
В общем случае это не так, т. е. вариантов
.
В общем случае это не так, т. е. вариантов![]() ,
превосходящих вариант
,
превосходящих вариант![]() по
простому большинству голосов, может
быть несколько. ■
по
простому большинству голосов, может
быть несколько. ■
21.7. Процедуры Нансона и Кумбса
Процедура Нансона (1882) объединяет подход Борда и принцип Кондорсе. Основная идея процедуры состоит в последовательном сокращении множества вариантов путем исключения получивших минимальное число голосов до тех пор, пока не останутся неисключаемые варианты. Эти варианты и будут считаться результатом коллективного выбора.
1
— 3. Совпадают с шагами 1 — 3 процедуры
Борда. Вместо шага 1 каждый участник
может провести попарные сравнения всех
вариантов![]() друг
с другом и по матрице парных
друг
с другом и по матрице парных
сравнений упорядочить все варианты.
4.
Определяется вариант![]() ,
соответствующий минимальному значению
функции Борда,
,
соответствующий минимальному значению
функции Борда,
![]()
G |
А |
В |
С |
Id |
А |
— |
33 |
25 |
5 |
В |
27 |
— |
42 |
3 |
С |
35 |
18 |
— |
12 |
5.
Повторяются шаги 1 — 4, и на суженном
множестве Ai
=
![]() вариантов
находится следующий вариант А2
, имею
вариантов
находится следующий вариант А2
, имею
щий минимальное число голосов, который исключается из рассмотрения.
6. Шаги 1 — 4 повторяются, пока не останется один или несколько вариантов, которые дальше нельзя исключить. Оставшиеся наиболее предпочтительные варианты составляют множество A*, определяемое функцией Нансона:
![]()
В модификации процедуры Нансона из рассмотрения исключается не единственный вариант, имеющий минимальную оценку Борда, а сразу несколько вариантов, оценки которых меньше среднего по всем вариантам значения функции Борда
![]()
![]()
Процедура Кумбса (1950) аналогична процедуре Нансона, но в ней последовательно исключаются из рассмотрения варианты, которые считаются худшими по большинству голосов.
Пример 21.6. Пусть выполняются условия примера 21.1. Распределение голосов избирателей при упорядочении кандидатов А, В и С имеет вид:
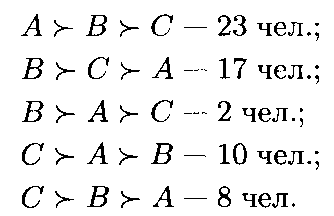
Значения функции Борда для каждого кандидата:
![]()
![]()
Кандидат
С, имеющий наименьшее значение функции
Борда, исключается. Индивидуальные
предпочтения избирателей на оставшемся
множестве кандидатов![]() =
=![]() выглядят
следующим образом:
выглядят
следующим образом:
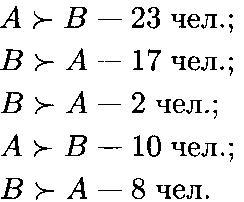
Вычислим новые значения функции Борда для каждого оставшегося кандидата Ал В, полагая, что в каждом индивидуальном упорядочении первому кандидату присваивается 1 бал Л, а второму кандидату — 0 баллов: /
![]()
Кандидат
В, имеющий наименьшее значение функции
Борда, исключается. Новое множество
кандидатов А2
состоит из единственного кандидата
А, который и является лучшим. Упорядочение
кандидатов в соответствии с функцией
Нансона
fn
имеет вид![]() и
отличается от результата, полученного
с помо
и
отличается от результата, полученного
с помо
щью функции Борда. ■
21.8. Процедуры Коупленда и Фишберна
Рассмотрим ряд процедур коллективного выбора, основанных на использовании неранжирующей процедуры учета мнений избирателей. В основе процедуры Коупленда (1950) лежит идея учета различия индивидуальных предпочтений участников, аналогичная идее модифицированной процедуры Борда. Однако здесь различие определяется не количеством голосов, поданных за более и менее предпочтительные варианты, а числом самих более или менее предпочтительных вариантов.
Каждый участник сравнивает все варианты
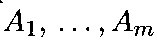 попарно
друг с другом независимо от сравнений
других пар вариантов.
попарно
друг с другом независимо от сравнений
других пар вариантов.Для каждого варианта Ai подсчитывается число
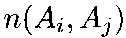 вариантов Aj,
уступающих
варианту
Ai,
и
число
n(Aj,
Ai)
варианта
Aj,
превосходящих вариант Ai
по
простому большинству голосов.
вариантов Aj,
уступающих
варианту
Ai,
и
число
n(Aj,
Ai)
варианта
Aj,
превосходящих вариант Ai
по
простому большинству голосов.Для каждого варианта Ai вычисляется значение функции Коупленда
![]()
равное разности числа вариантов Aj, которые уступают варианту Ai, и числа вариантов Aj, которые превосходят вариант Ai по простому большинству голосов.
Упорядочение вариантов строится по убыванию значения функции Коупленда
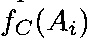 .
Лучший вариант А* определяется
максимальным значением функции Коупленда
.
Лучший вариант А* определяется
максимальным значением функции Коупленда
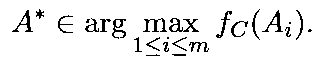
Заметим, что получающееся итоговое упорядочение может быть как строгим, так и нестрогим.
Процедура Фишберна (1970) объединяет идеи процедур Борда, Кондорсе и Коупленда, определяя предпочтительность каждого варианта по числу вариантов, которые данный вариант превосходит по простому большинству голосов.
Совпадает с шагом 1 процедуры Коупленда.
Для каждого варианта Ai вычисляется значение функции Фишберна
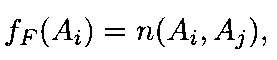
равное числу вариантов Aj, которые уступают варианту Ai по простому большинству голосов.
Упорядочение вариантов строится по убыванию значения функции Фишберна
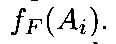 Лучший
вариант Л* определяется максимальным
значением функции Фишберна
Лучший
вариант Л* определяется максимальным
значением функции Фишберна
![]()
Пример 21.7. Пусть выполняются условия примера 21.1 и голоса избирателей при попарном сравнении кандидатов А, В и С распределились так:
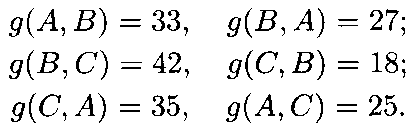
Вычислим
значения функции Коупленда![]() для
каждого из кандидатов
А, В
и
С.
Кандидат
А
превосходит по простому большинству
голосов (первая колонка) только одного
кандидата В
и уступает только одному кандидату
С.
Поэтому
для
каждого из кандидатов
А, В
и
С.
Кандидат
А
превосходит по простому большинству
голосов (первая колонка) только одного
кандидата В
и уступает только одному кандидату
С.
Поэтому![]() 1
—
1
—
—
1
= 0. Кандидат
В
превосходит одного кандидата
С
и уступает одному кандидату А,
поэтому![]() =1
— 1 = 0. Аналогично, для кандидата
С
имеем
=1
— 1 = 0. Аналогично, для кандидата
С
имеем![]() =1
— 1 = 0. Таким образом, все три кандидата
А, В
и
С
эквивалентны. Лучшего кандидата по
функции Коупленда
=1
— 1 = 0. Таким образом, все три кандидата
А, В
и
С
эквивалентны. Лучшего кандидата по
функции Коупленда![]() нет.
нет.
Вычислим
значение функции Фишберна fp
для
каждого из кандидатов
А,
В
и С. Кандидат
А
превосходит по простому большинству
голосов только одного кандидата
jB,
и![]() =
1.
=
1.
Аналогично,![]() =
1 и
=
1 и![]() =1.
Итак, все три кандидата А,
=1.
Итак, все три кандидата А,
В
и
С
эквивалентны. Лучшего кандидата по
функции Фишберна![]() нет. ■
нет. ■
