2.2. Способ представления фал с использованием карт Вейча – Карно

Способ представления с использованием карт Вейча – Карно базируется на табличном представлении ФАЛ. Такой способ используется для ручной минимизации, когда количество входных переменных не более пяти.

Карта Вейча – Карно – это прямоугольная таблица, число клеток в которой равно 2ⁿ, где n – число переменных. Для каждой клетки ставится в соответствие свой набор входных переменных, а в клетке записывается значение функции (0 или 1) на этом наборе.

К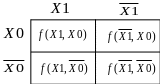 арта для двух входных переменных представлена на рис. 2.1. Она содержит четыре клетки. По краям карты указаны значения входных переменных, которые не изменяются для соответствующих строк и столбцов.

Рис. 2.1. Карта Вейча – Карно для функции двух переменных

К арта для трёх входных переменных представлена на рис. 2.2. Она содержит восемь клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов являются соседними, поэтому пространственно такая карта может быть представлена в виде цилиндра.

Рис. 2.2. Карта Вейча – Карно для функции трёх переменных

Карта для четырёх входных переменных представлена на рис. 2.3. Она содержит шестнадцать клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена в виде тора.

Карта для пяти входных переменных содержит тридцать две клетки. Её можно представить как две карты для четырёх переменных, расположенные одна над другой. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена как два тора, вложенные один в другой. Соседним наборам дополнительно соответствуют клетки, расположенные на разных торах одна под другой. Ввиду сложности работы с такой картой она применяется достаточно редко.

Р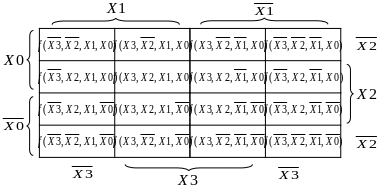 ис. 2.3. Карта Вейча – Карно для функции четырёх переменных

2.3. Минимизация полностью определённой фал

При минимизации ФАЛ с помощью карт Вейча – Карно используются либо единичные, либо нулевые значения функции. В обоих случаях получаются равносильные выражения, которые, однако, могут отличаться по числу ЛЭ и выполняемым логическим операциям.

В п. 1.5 отмечено, что ФАЛ называется полностью определённой, если заданы все 2ⁿ её значений y_i. Алгоритм минимизации такой ФАЛ с помощью карт Вейча – Карно следующий:

1) на карте, построенной для ФАЛ, содержащей n-переменных, выделяют прямоугольные области, объединяющие выбранные значения (0 или 1) функции. Каждая область может содержать только 2^k клеток, где k – целое число. Выделенные области могут пересекаться, то есть одна или несколько клеток могут принадлежать разным областям.

2) каждой из выделенных областей соответствует самостоятельное логическое произведение входных переменных, значения которых в пределах выделенной области остаются неизменными. Каждое такое произведение содержит (n – k) переменных и называется импликанта.

3) из полученного множества областей выбирают минимальное число максимально больших, включающих в себя все выбранные значения (0 или 1) функции.

4) логически суммируются импликанты, соответствующие выбранным областям. Полученная функция образует МДНФ.

При объединении клеток с единичными значениями ФАЛ получается МДНФ самой функции, а при объединении клеток с нулевыми значениями – МДНФ функции, инверсной заданной.

Применив к полученной инверсной МДНФ теоремы Де-Моргана можно получить минимальную конъюнктивно нормальную функцию (МКНФ).

Рассмотрим пример минимизации ФАЛ, заданной алгебраическим выражением:

. (2.3)

С оставим карту Вейча – Карно для заданной ФАЛ.

Выделим на карте покрытие, содержащее все единичные значения ФАЛ (выделено пунктиром). Запишем для него значение импликанты, которая будет единственным слагаемым в МДНФ: Y = X2.

Если объединить нулевые значения функции (выделено штрих пунктиром), получим МДНФ, инверсную заданной: или Y = X2. В данном простом примере в обоих случаях получилось одно и то же выражение.

Рассмотрим другой пример минимизации ФАЛ, заданной алгебраическим выражением [1]:

. (2.4)

С оставим карту Вейча – Карно.

Выделим на карте две области, содержащие все единичные значения ФАЛ (выделено пунктиром). Запишем МДНФ как логическую сумму двух импликант: .

Выделим на карте две области, содержащие все нулевые значения ФАЛ (выделено штрих пунктиром). Запишем МДНФ, инверсную заданной, как логическую сумму двух импликант: .

Получились равносильные, но разные выражения. Чтобы доказать равносильность выражений, применим к МДНФ, инверсной заданной, теорему Де-Моргана:

.

Применив к данному выражению теорему №10 (см таблицу 1.7), получим ФАЛ .

Даже из таких простых примеров видно, что при минимизации по единичным и по нулевым значениям получаются равносильные, но не обязательно одинаковые выражения. Техническая реализация таких логических устройств также будет различной. Используя теоремы алгебры логики выражения можно преобразовать к одинаковому виду, однако преобразования могут быть не очевидны. Поэтому при минимизации желательно рассмотреть оба варианта значений функции и постараться получить наиболее простое выражение, которое будет иметь минимальную стоимость технической реализации.