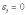- •1.3. Реология
- •4.2. Контроль за угоном плетей и изменениями температурного режима их работы
- •Техническая характеристика
- •3.1. Расчет расхождения торцов рельсов в месте разрыва рельсовой плети и увеличения начальных стыковых зазоров в уравнительных пролетах
- •3.5.1 Расчет расхождения торцов рельсов в месте разрыва рельсовой плети
- •Особенности устройства и работы бесстыкового пути
- •3.3. Повышение сопротивления железобетонных шпал сдвигу поперек оси пути
- •Определение относительной скорости неупругого скольжения колеса по рельсу
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 1
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 2
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 3
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 4
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 5
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 6
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 7
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 8
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 9
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 10
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 11
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 12
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 13
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 14
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 16
Зав. кафедрой П.Н. Щербак |
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 17
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 18
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 19
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 20
Зав. кафедрой П.Н. Щербак
|
Кафедра «Путь и путевое хозяйство» РГУПС Дисциплина «Расчеты и проектирование элементов железнодорожного пути» ______________ экзаменац. сессии 2010/2011 уч. года
Б И Л Е Т № 15
Зав. кафедрой П.Н. Щербак
|
1.1. Первые методы оценки устойчивости пути с длинными рельсами появились еще в XIX веке. Они отражали лишь какой-то определенный этап работы конструкции, который был исследован разработчиками опытным путем. После появления бесстыкового пути со сварными стыками возникла необходимость разработки теории его работы, которая бы реально отражала его состояние в процессе эксплуатации.
Начало теоретических исследований устойчивости бесстыкового пути относится к 1913 г. В последующие годы были созданы разные варианты методов расчета величин продольных критических сил в рельсах: энергетический, интегральных уравнений, дифференциальных уравнений и др. Значительный вклад в решение этих вопросов внесли российские ученые: В.Г. Альбрехт, М.С. Боченков, Е.М. Бромберг, М.Ф. Вериго, Н.П. Виногоров, В.А. Грищенко, Н.Б. Зверев, Э.П. Исаенко, Н.И. Карпущенко, С.И. Клинов, А.Я. Коган, А.А. Кривобородов, К.Н. Мищенко, С.И. Морозов, В.И. Новакович, С.П. Першин и другие, а так же зарубежные ученые: О. Амман, М. Балух, К. Грюневальдт, Д. Игнятич, Г. Майер, Нгуен Ван Туен, И. Немешди-Немшек, Э. Немежди и другие. В каждом из предложенных методов сделаны, упрощающие расчетную схему допущения, приняты различные формы деформаций рельсов в плане до выброса, имеются различия в исходных уравнениях равновесия и в величинах задаваемых исходных данных.
Метод дифференциальных уравнений равновесия. Данный класс методов более точен, так как уравнением упругой линии уже не задаются, а оно выводится в ходе решения и полностью соответствует схеме нагружения [1,2].
Основное дифференциальное уравнение изгиба имеет вид:
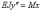 (1)
(1)
Зная выражение для изгибающего момента Мх в любом сечении деформированного пути, получают дифференциальное уравнение в развернутом виде. При этом по концам стержня приходится вводить опорные реакции и опорные моменты.
Методом дифференциальных уравнений пользовались многие ученые, как в России, так и за рубежом, начиная с начала XX столетия.
Р. Леви составил систему уравнений, симметричной половины волны, предполагая, что при волнообразном искривлении реакция балласта в двух крайних четвертях волны уравновешиваются реакциями двух средних четвертей.
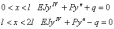 (2)
(2)
С.И. Морозов предложил расчет устойчивости бесстыкового пути, использующий дифференциальное уравнение изгиба балки:
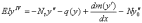 (3)
(3)
где q(y), m(y') - реактивная сила и момент; у, у0 - ординаты прогиба и начальных неровностей оси рельсошпальной решетки.
В. И. Новакович предложил использовать элементы теории ползучести при расчетах бесстыкового пути методом дифференциальных уравнений [3].
Д. Игнятич, впервые ввел в дифференциальные уравнения устойчивости пути неравномерность распределения сил сопротивления рельсошпальной решетки по длине пути, а так же учел в расчетах начальные неровности пути и неравномерность нагрева плетей [4].
Наиболее полное решение по определению устойчивости бесстыкового пути методом дифференциальных уравнений дано в работах [1,2].
В основу положена расчетная схема, изображенная на рис. 1.
Поставленная задача была решена при следующих допущениях:
1) продольные силы в обеих нитях одинаковы и постоянны N = const, величина продольной силы при этом равна полусумме фактически действующих в обеих рельсовых нитях сил;
2)
радиус кривизны обеих нитей один и тот
же 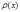 ,
при этом кривизна
,
при этом кривизна  равна
полусумме кривизны наружной и внутренней
нитей;
равна
полусумме кривизны наружной и внутренней
нитей;
3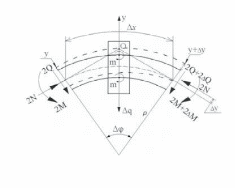 )
при деформации пути шпалы перемещаются
параллельно сами себе.
)
при деформации пути шпалы перемещаются
параллельно сами себе.
Рисунок 1 - Расчетная схема пути при использовании уравнения упругой оси
Как следует из второго предположения, изгибающий момент и поперечная сила в обеих рельсовых нитях одинакова.
Вырежем
элемент пути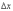 ,
размером, равным расстоянию между
соседними шпалами и рассмотрим его
равновесие.
,
размером, равным расстоянию между
соседними шпалами и рассмотрим его
равновесие.
Составляя сумму моментов относительно точки О, получим:
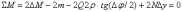 (4)
(4)
где 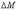 -
приращение изгибающего момента в рельсе
на длине
-
приращение изгибающего момента в рельсе
на длине
m - момент, прикладываемый к рельсу со стороны скрепления
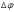 -
угол, стягивающий дугу
-
угол, стягивающий дугу
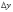 -
приращение поперечного перемещения
рельса на дуге
-
приращение поперечного перемещения
рельса на дуге
Деля равенство (5) на величину 2 и учитывая соотношение:
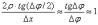 (5)
(5)
получим равенство
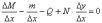 (6)
(6)
Учитывая приближенные равенства отношений приращений, и отношений дифференциалов и вводя обозначение,
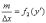 (7)
(7)
которое выражает тот факт, что момент m, приложенный от скрепления к рельсу, зависит от угла скручивания рельса относительно шпалы, получим:
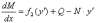 (8)
(8)
Составим сумму проекций сил на вертикальную ось:
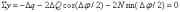 (9)
(9)
где 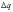 -
сила, передаваемая на рельсы от шпалы
-
сила, передаваемая на рельсы от шпалы
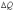 -
приращение поперечной силы на дуге
-
приращение поперечной силы на дуге
Деля равенство (9) на величину 2 и учитывая соотношение:
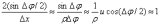 (10)
(10)
получим
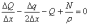 (11)
(11)
Теперь, заменяя отношение приращений отношением дифференциалов и вводя функцию:
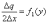 (12)
(12)
согласно которой сила, приложенная к рельсу со стороны шпалы, зависит от перемещения, получим:
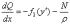 (13)
(13)
Дифференцируя выражение (12) и подставляя значение Q из формулы (11) получим:
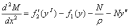 (14)
(14)
Теперь воспользуемся соотношением, определяющим момент в кривом стержне:
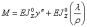 (15)
(15)
Е - модуль упругости рельсовой стали
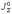 -
момент инерции рельса относительно
главной вертикальной оси
-
момент инерции рельса относительно
главной вертикальной оси
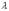 -
продольное перемещение сечения рельса
-
продольное перемещение сечения рельса
Вторым членом в соотношении (15) можно пренебречь в связи с его малостью. С учетом всего вышесказанного получим следующее выражение:
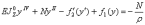 (16)
(16)
Кривизну
рельса
,
представляем в виде суммы кривизны
круговой кривой 1/R,
(R-радиус
круговой кривой) и кривизны начальной
неровности пути 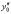
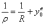 (17)
(17)
После
подстановки: 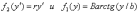 получим
основное уравнение устойчивости
бесстыкового пути:
получим
основное уравнение устойчивости
бесстыкового пути:
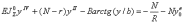 (18)
(18)
где R - радиус кривой
r, В, b- эмпирические коэффициенты к функциям сопротивлений
Это уравнение, без учета начальных неровностей, решается следующей системой трансцендентных нелинейных уравнений:
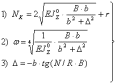 (19)
(19)
Данный метод позволяет определить критическое состояние пути при заданных параметрах. Точность решения при использовании этого метода зависит только от точности аппроксимации коэффициентов к функциям различных сопротивлений.
В полном решении возможен учет начальных напряженных и ненапряженных неровностей, неравномерности распределения сопротивлений по длине пути (неравномерность затяжки клеммных болтов и места с оголенными концами шпал), эксцентриситет приложения продольных сил и.т.д.
1.2. Температура рельсов и температура закрепления плети Основное отличие в работе бесстыкового пути от звеньевого заключа-ется в том, что в плетях действуют значительные силы, зависящие от измене-ния температуры рельсов. Температура рельсов зависит от многих факторов: температуры возду-ха, типа рельса и состояния его поверхностей, а также ориентирования рельса относительно сторон света, плана и профиля пути; поперечного профиля земляного полотна (насыпь, выемка, нулевое место), интенсивности солнеч-ной радиации и прозрачности атмосферы, скорости и направления ветра, ка-чества и отражательной способности балласта и ряда других причин. При одной и той же температуре воздуха и различных сочетаниях дру-гих перечисленных факторов температура рельсов на одном и том же пере-гоне может быть разной. Причем отличие температур в зависимости от усло-вий может достигать 10-15°С и более. Температура рельсов летом в дневные часы, как правило, выше темпе-ратуры воздуха. За расчетную разницу температур между ними летом в на-стоящее время принимают 20°С, т.е. tp = tв + 20°С, где tp – температура рельса; tв – температура воздуха. Зимой температура рельсов меньше отличается от температуры возду-ха. При экстремальных зимних температурах воздуха (-30°С и ниже) их тем-пература может быть на 3-5°С выше, а из-за выхолаживания при сильном ветре температура рельсов может быть и ниже температуры воздуха. Однако обычно зимой температура рельсов и воздуха совпадает и в расчетах прини-мают tp = tв. При повышении температуры рельсовых плетей по сравнению с темпе-ратурой закрепления в них возникают продольные силы сжатия, которые мо-гут создать опасность выброса пути. При понижении температуры — появ-ляются растягивающие силы, которые могут вызвать излом плети и образо-вание большого зазора, опасного для прохода поезда, или разрыв рельсового стыка из-за среза болтов. Нейтральной температурой является та, при кото-рой в рельсовых плетях отсутствуют продольные силы и соответствующие им напряжения – температура закрепления плети. При изготовлении и укладке рельсовых плетей, производстве работ по техническому обслуживанию и ремонту бесстыкового пути измеряют факти-ческую температуру рельсов. В настоящее время таковой принято считать температуру головки рельса. Впервые температура рельсовой плети измеря-ется на рельсосварочном предприятии, где определяется та, при которой из-готовлена плеть. После укладки рельсовой плети в путь температуру рельсов при закре-плении плетей на шпалах измеряют дважды – перед началом и после оконча-ния закрепления. Для сокращения интервала изменения температуры рельсо-вых плетей сначала их закрепляют на каждой пятой шпале. 2.2. Температурные напряжения в плетях бесстыкового пути С момента закрепления рельсовой плети на постоянный режим начина-ется «температурная жизнь» плети. Если рельс не может изменять длину при колебаниях своей темпера-туры, то в нем возникают температурные силы Pt, прямо пропорциональные изменению температуры рельса относительно нейтральной температуры и не зависящие от длины рельса L. Рис. 2.1. Распределение продольной температурной силы по длине рельса: L – общая длина рельса; x – длина подвижной части рельса; (L-2x) – непод-вижная часть рельса; Rс – стыковое сопротивление. В рельсовом стыке накладки, стянутые болтами, создают силу сопро-тивления смещению конца рельса в стыке. Очевидно, что процесс изменения длины рельса не сможет начаться, пока возникающая при изменении темпе-ратуры рельса продольная температурная сила не превысит силу стыкового сопротивления (Rс). Стыковое сопротивление зависит от чистоты поверхно-сти накладок и рельсов, количества стыковых болтов и их затяжки.
1.3. Реология
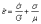
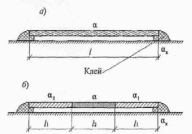
(точка означает производную по времени). Если задано напряжение как функция времени, t, то скорость деформации легко находится по формуле
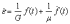
Если же деформация задана как функция времени, то реологическое уравнение Максвелла представляет собой дифференциальное уравнение относительно , решение которого имеет вид
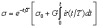
(здесь –
начальное напряжение при t
= 0,
а величина 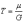 называется
временем релаксации). Пусть в начальный
момент к образцу прикладывается усилие,
вызывающее напряжение ;
при этом в образце возникает деформация .
Если эту деформацию поддерживать
постоянной, (,
то напряжение ,
согласно (2), убывает со временем
экспоненциально, т.е.
называется
временем релаксации). Пусть в начальный
момент к образцу прикладывается усилие,
вызывающее напряжение ;
при этом в образце возникает деформация .
Если эту деформацию поддерживать
постоянной, (,
то напряжение ,
согласно (2), убывает со временем
экспоненциально, т.е.
е\up12–t/T
и за время T уменьшается в e раз, (e – основание натуральных логарифмов). Таким образом, время релаксации T характеризует скорость убывания напряжений в описанном процессе при const, который называется процессом релаксации.
Реологическое уравнение Максвелла пригодно для качественного описания процессов в стекловидных и полимерных материалах. Для хорошего количественного описания используются более сложные модели.
Выражение для f(t) содержит интеграл по времени от начала процесса до текущего момента; поэтому значение напряжения в момент t зависит от значений во все предшествующие моменты от 0 до t, поэтому такие модели называют «материалами с памятью».
Для описания реологических свойств суглинка, имеющего структуру геля, в котором частицы песка соединяются цепочками коллоидных частиц глины, а промежутки заполнены водой, Кельвин предложил схему, в которой упругий и вязкий элементы соединены параллельно, т.е. так, что их деформации одинаковы (рис. 4).
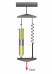
Соответствующее реологическое уравнение получается аналогично тому, как это сделано для среды Максвелла, но с учетом того, что в модели Кельвина одинаковы деформации элементов, а общее напряжение получается суммированием напряжений в вязком и упругом элементах:
G
Анализ показывает, что среда Кельвина является твердым телом, похожим на губку, пропитанную вязкой жидкостью.
Примером более сложной модели является среда Бингама, модель которой представлена на рис. 4. Если увеличивать силу P, то сначала деформируется только пружина; затем, при определенном значении силыP, преодолевается сила трения бруска о поверхность и начинается его движение, сопротивление которому оказывает не только трение, но и вязкое сопротивление поршня в цилиндре (рис. 5).
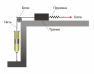
Считается, что реология началась именно с этой модели, не укладывающейся в рамки взаимодействия классических сред – упругого тела и вязкой жидкости. Среда Бингама была введена для описания поведения свежей масляной краски, когда было установлено, что она является пластическим твердым телом, а не вязкой жидкостью.
Реологические модели, получаемые путем комбинирования основных элементов (упругость, вязкость, трение) качественно описывают поведение под нагрузкой реальных сред, но наблюдаются при этом значительные количественные отклонения. Но известны эффекты, для описания которых в настоящее время еще не создана удовлетворительная теория. В первую очередь, это так называемый эффект Вайсенберга. Он проявляется, в частности, в следующем опыте (рис. 6): Пусть есть два одинаковых стакана – один с ньютоновской вязкой жидкостью, например, с растительным маслом, другой – с концентрированным раствором высокополимерного вещества (например, сладкого сгущенного молока); оба стакана приводятся во вращение вокруг своих осей. Сверху в стаканы опущены неподвижные круглые стержни. В стакане с маслом видна ожидаемая картина – жидкость принимает форму тела вращения с параболической поверхностью, вертикальная координата которой возрастает с удалением от центра. Но в другом стакане жидкость начнет медленно подниматься по центральному неподвижному стержню, в результате чего уровень поверхности у оси оказывается выше, чем у краев.
Не менее интересен и «эффект Томса». В 1940-х многие исследователи замечали, что течение жидкости по трубопроводу сильно облегчается (снижается гидравлическое сопротивление), если в низкомолекулярную жидкость добавить очень малое (доли процента) количество растворимого полимера. Оказалось, что можно достигнуть четырехкратного снижения гидравлического сопротивления воды в трубе, добавляя несколько миллионных долей (по весу) подходящего высокомолекулярного вещества. Этот эффект используется в некоторых нефтепроводах, пожарных шлангах; есть исследования по снижению кровяного давления у животных.
Изучение реальных сред со сложными свойствами не обязательно относят к реологии: теория неньютоновской жидкостей, теория вязкоупругости и вязкопластичности, теория ползучести металлов при высоких температурах, механика природных процессов – это самостоятельные научные направления, с которыми связаны многие важнейшие достижения как в области теории, так и в области практики – от медицины до космоса, от снежных лавин до дрейфа континентов.
2.1. Бесстыковой путь температурно-напряженного типа – это путь со сварными рельсовыми плетями такой длины, при которой даже в период наибольших изменений температуры рельсов по сравнению с нейтральной tз рельс, преодолев сопротивления стыковых скреплений Rc, не сможет полностью преодолеть погонное сопротивление r продольному перемещению (зимние rз = 2,12,5 т/м или летние rл = 0,71,2 т/м) на всей своей длине.
В бесстыковом пути (в отличие от звеньевого) продольные возвратно-поступательные перемещения рельсошпальной решётки (при талом балласте) и рельсов по прокладкам (при замёрзшем балласте) имеют место только на концевых участках плети. Средняя часть плети остается всегда неподвижной.
Изменение температуры рельсов (t) по сравнению с нейтральной (tз – температура закрепления плети) приводит к появлению в плетях продольных температурных сил
Nt = E Fp t, |
(3.1) |
где – коэффициент линейного расширения рельсовой стали, равный 0,0000118 1/С; Е – модуль упругости рельсовой стали, Е = 2,1∙106 кг/см2; Fр – площадь поперечного сечения рельса, см2; t – изменение температуры рельса, С.
При повышении температуры в рельсовых плетях будут возникать сжимающие продольные температурные силы (–Nt), а при понижении – растягивающие (+Nt). Подставляя в формулу (3.1) численные значения , Е и площадь поперечного сечения рельса типа Р65 (Fр = 82,7 см2) получим
Nt = 20,7 t (кН) или Nt = 2,07 t (т). |
(3.2) |
Из уравнений 3.1 и 3.2 видно, что продольная температурная сила (±Nt ) зависит только от изменения температуры рельса относительно температуры закрепления (tз) и типа рельса, а именно от площади поперечного сечения рельса (Fр).
В бесстыковом пути (с новыми рельсами Р65) изменение температуры рельса на 1С вызывает в его неподвижной части продольную температурную силу Nt ≈ 2,07 т.
При этом величина температурных напряжений в средней (неподвижной) части плети в связи с несостоявшимся изменением ее длины определяется как
|
|
или |
(3.3) |
t = E t. |
|
Подставляя в формулу (3.3) численные значения коэффициента линейного расширения рельсовой стали и модуля упругости рельсовой стали Е, получим
|
(3.4) |
Из этого следует, что нормальные температурные напряжения в неподвижной части плети не зависят от типа рельса и длины рельсовой плети, а изменение температуры бесстыковой плети на каждый 1С вызывает в его неподвижной части изменение температурного напряжения t на 25 кг/см2 или на 2,5 МПа.
Сжимающие температурные напряжения при повышении температуры плети относительно нейтральной (-t лето) и растягивающие при понижении температуры (+t зима), равномерно распределены по поперечному сечению рельса (рис. 3.2. а).
Известно что, в конструкции бесстыкового пути применяют разнородные материалы: сталь, железобетон, щебень (или другой вид балласта), резина (или пластмасса). Все эти материалы взаимно связаны, и в местах их соприкосновения при действии внешних активных сил возникают реактивные силы, обусловленные связями между составными частями пути. Эти силы называют сопротивлениями перемещению частей бесстыкового пути относительно друг друга. Они действуют в продольном, боковом и вертикальном направлениях.
Сопротивления продольным перемещениям пути – определяющий фактор в его температурной работе. Эти сопротивления оказывают стыковые соединения плетей и отдельные опоры, совместно с балластным слоем.
Стыковое сопротивление Rc - это сосредоточенная сила трения рельсов в накладках. Сопротивление стыка продольному перемещению рельса зависит от чистоты поверхностей накладок и рельсов, количества и качества стыковых болтов, силы затяжки их, конфигурации накладок.
Погонное сопротивление r – это сопротивление отдельных опор продольному перемещению рельсов. Для удобства расчётов реактивные сосредоточенные силы на каждой отдельной опоре заменяют погонными, приходящимися в среднем на 1 м (или 1 см) пути одной рельсовой нити.
Величина погонного сопротивления зависит: от типа, эпюры, состояния и конфигурации шпал; рода, количества, качества и состояния балласта (степени его уплотнения, загрязнения и увлажнения); конструкции промежуточных скреплений; климатических условий (влажности, температуры); времени года; качества содержания пути и т.д. Выделить влияние каждого фактора и точно его оценить трудно, поэтому погонное сопротивление определяется экспериментально.
Следует различать зимнее (rз) и летнее (rл) погонное сопротивление. В летнее время продольные смещения рельсов могут происходить вместе со шпалами по балласту, так как сопротивление сдвигу рельсов в зоне промежуточных скреплений в 3 – 4 раза превышает сопротивление сдвигу самих шпал в балласте. В зимнее время при смёрзшемся балласте возможны перемещения рельсов, преодолевающих сопротивления в узлах промежуточных скреплений.
Сопротивления зависят не только от конструкции элементов пути, но и от их состояния и текущего содержания. В расчётах принимают сопротивления нового пути, а в процессе эксплуатации поддерживают их на начальном уровне.
Стыковое сопротивление (Rс) стыков с рельсами Р65 с двухголовыми шестидырными накладками с болтами нормальной прочности (с временным сопротивлением на разрыв 735 МПа), изготовленных из стали марки 35, равно 400 ÷ 420 кН. При этом, гайки шести стыковых болтов должны быть затянуты с крутящим моментом не менее 600 Н∙м (60 кгс∙м).
При наличии высокопрочных стыковых болтов из легированной рельсовой стали (с временным сопротивлением на разрыв 833 МПа), марки 40Х и накладок шарнирного типа, максимальное стыковое сопротивление Rс = 700 ÷ 800 кН. При этом гайки стыковых болтов затягивают с крутящим моментом Мкр=1100 Н∙м (110 кгс∙м).
В расчетах бесстыкового пути на прочность стыковое сопротивление Rc=Rб (бытовому) принимают равным 140 ÷ 160 кН (14 ÷ 16 т∙с).
Летние погонные сопротивления (rл) продольным перемещениям в соответствии с указанием МПС от 22.12.2000 №C-3112У равны: для пути с рыхлым балластным слоем (вновь уложенным) rл = 0,7 тс/м = 7 кН/м = 7 н/мм; для балласта, уплотненного динамическим стабилизатором rл = 0,9 тс/м = 9 кН/м =9 Н/мм; для стабилизированного пути, пропустившего более 50 млн.т.бр rл = 1 ÷ 1,25 тс/м = 10 ÷ 12,5 кН/м = 10 ÷ 12,5 Н/мм.
Зимнее погонное сопротивление (rз) продольным перемещениям рельсов по прокладкам промежуточных рельсовых скреплений начинает действовать при температуре воздуха tз = –5 ÷ –10°С, т.е. при замерзшем балластном слое. Для обеспечения требуемого погонного сопротивления нормативное прижатие рельса должно составлять не менее 20 кН.
При скреплении КБ-65 это достигается при среднем нормативном усилии затяжки гаек клеммных и закладных болтов (одновременно с затяжкой выполняется смазывание резьбы болтов и гаек), с соответствующим крутящим моментом равным 200 Н∙м (20 кгс∙м) и 150 Н∙м (15 кгс∙м) при этом погонное сопротивление (продольным перемещениям рельсов по прокладкам промежуточных скреплений) будет равно rзКБ = 2,5 тс/м = 25 кН/м = 25 н/мм.
Во избежание угона плетей средний крутящий момент затяжки гаек клеммных и закладных болтов соответственно должен быть не менее 100 Н∙м (10 кгс∙м) и 70 Н∙м (7 кгс∙м).
При скреплениях ЖБР-65 крутящий момент, приложенный к гайке закладного болта равен 180 ÷ 200 Н∙м (18 ÷ 20 кг∙м).
При скреплении ЖБР-65Ш крутящий момент, приложенный к головке шурупа должен быть не менее 220 ÷ 250 Н∙м (22 ÷ 25 кг∙м).
При этом максимальное зимнее погонное сопротивление rз:
в кривых R≤ 1200 м – rзЖБР-65 = 2,3 тс/м = 23 кН/м = 23 н/мм,
в кривых R > 1200м и в прямых – rзЖБР-65 = 2,1 тс/м = 21 кН/м = 21 н/мм.
В скреплениях АРС сила прижатия рельса к шпале зависит от позиции монорегулятора при III–ей позиции – 1000 кгс, IV-ой – 1200 кгс.
Итак, в бесстыковых плетях действуют продольные температурные силы (±Nt) и силы сопротивления им (стыковые и погонные). Температурные силы не в состоянии преодолеть силы сопротивления по всей длине рельса. Силы сопротивления продольному сдвигу рельсов преодолеваются только на двух концевых участках, которые называют температурно-подвижными («дышашими»), а в средней части бесстыковой плети всегда имеется неподвижный отрезок той или иной длины.
2.2. В рельсовых плетях бесстыкового пути при изменении температуры возникают значительные продольные силы за счет несостоявшегося удлинения рельсов. С учетом температурной деформации закон Гука можно записать в виде:
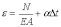 (1)
(1)
где N-
продольная сила в рельсе, Е -
модуль упругости металла, А -
площадь поперечного сечения рельса,  -
коэффициент температурного расширения
стали,
-
коэффициент температурного расширения
стали, 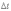 -
изменение температуры рельса.
-
изменение температуры рельса.
Считая, что средняя часть рельсовой плети не деформируется (е=0), можно найти продольную силу, возникающую при изменении температуры:
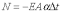 (2)
(2)
Расчет показывает, что при изменении температуры рельса на 1°С, напряжения изменяются на 2,5 МПа, а продольная сила - на 20 кН (на одну нить рельса Р65). В существующих вКазахстане климатических условиях рельс может охлаждаться на 70°С относительно температуры закрепления, при этом растягивающая продольная сила может достигать значения 1400 кН. Нагрев рельса выше температуры закрепления меньше, (максимум около 30°С), при этом возникает продольная сжимающая сила порядка 600 кН.
Наличие продольных сил в рельсах - основной недостаток бесстыкового пути. Летом, при повышенных температурах путь может потерять устойчивость, а зимой, при пониженных температурах возможно разрушение рельса с разрывом плети.
Другой причиной появления продольных сил является угон пути - необратимое продольное перемещение рельсов при движении вертикальной нагрузки. Эти усилия невелики по сравнению с температурными, их значения, как правило, не более 100 кН.
В настоящее время нет простого и надежного способа измерения усилий в рельсе, поэтому их определяют косвенно, по температуре. При этом возможны ошибки, которые появляются из-за несоответствия расчетной схемы и поведения реальной конструкции.
Впервые фотоупругие датчики (рис.1,а) для измерения напряжений в натурных конструкциях были применены в 1959г. [1]. Для снятия отсчетов применяются визуальные методы - метод полос, методы компенсации фотоупругой картины полос.
Однако эти датчики не являются термокомпенсированными, Они приклеиваются к конструкции только концами, что приводит к влиянию температуры на результаты измерения. Чтобы устранить влияние температуры на показания датчика можно дополнить его элементами термокомпенсации (рис. 1,б). При надлежащем выборе размеров датчика в зависимости от коэффициентов линейного расширения материалов, можно добиться того, что температурные деформации не влияют на показания датчика. Условие термокомпенсации можно записать в виде:
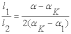
|
|
(3)
|
где: 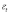 -
температурная компонента деформации
датчика, l
-
температурная компонента деформации
датчика, l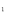 ,l
,l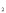 -
размеры элементов термокомпенсации и
датчика соответственно (рис.
1, б),
-
размеры элементов термокомпенсации и
датчика соответственно (рис.
1, б), 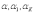 коэффициенты
температурного расширения материала
датчика, элементов термокомпенсации и
конструкции соответственно
коэффициенты
температурного расширения материала
датчика, элементов термокомпенсации и
конструкции соответственно
а) нетермокомпенсированный, б) термокомпенсированный
Рисунок 1- Фотоупругие датчики
У такого способа термокомпенсации есть недостаток: необходимо точное изготовление датчика.
Для устранения влияния температуры на показания датчика его можно приклеивать к рельсу по всей поверхности.
Деформации рельса определяются суммой силовой и температурной компонент:
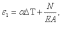
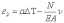 (4)
(4)
где:
-
коэффициент температурного расширения, 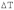 -
изменение температуры, Е - модуль
упругости,
-
изменение температуры, Е - модуль
упругости, -
коэффициент Пуассона, A- площадь
поперечного сечения рельса. Деформации
рельса и датчика одинаковы. Если на
рельс действует только продольная сила,
сдвиговая деформация равна нулю. При
прохождении поляризованного света
через напряженный фотоупругий датчик,
луч получает оптическую разность
хода
-
коэффициент Пуассона, A- площадь
поперечного сечения рельса. Деформации
рельса и датчика одинаковы. Если на
рельс действует только продольная сила,
сдвиговая деформация равна нулю. При
прохождении поляризованного света
через напряженный фотоупругий датчик,
луч получает оптическую разность
хода 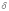 (ОРХ),
которая зависит от разности деформаций
[2]:
(ОРХ),
которая зависит от разности деформаций
[2]:
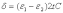 (5)
(5)
где: 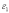 и
и  -
главные деформации датчика, t- толщина
датчика, С - оптикомеханическая постоянная
материала датчика.
-
главные деформации датчика, t- толщина
датчика, С - оптикомеханическая постоянная
материала датчика.
Подставим (4) в (5), получим:
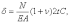
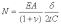 (6)
(6)
Выражения (6) не содержат изменения температуры, следовательно, фотоупругий датчик не требует дополнительной термокомпенсации. Так как все величины, входящие в (6), кроме ОРХ, известны или могут быть найдены из тарировочных испытаний и являются постоянными, то это выражение можно переписать в виде:
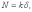
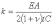 (7)
(7)
Значение ОРХ определяется с использованием специального прибора –
полярископа, собранного по V-образной схеме (рис.5)
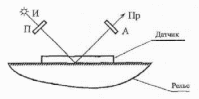
И-источник света, Пр –фотоприемник, П-поляризатор, А-анализатор
Рисунок 2-Схема V-образного полярископа для измерения усилий в рельсах
Интенсивность
света на выходе из скрещенного полярископа
I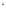 (плоскости
пропускания поляризатора и анализатора
ориентированы по отношению друг к другу
под углом 90°) определяется формулой
[2]:
(плоскости
пропускания поляризатора и анализатора
ориентированы по отношению друг к другу
под углом 90°) определяется формулой
[2]:
I=I 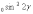 sin
sin 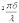 (8)
(8)
где:
I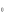 -
интенсивность света на входе полярископа
(обычно величина известная),
-
интенсивность света на входе полярископа
(обычно величина известная), 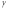 -
угол между направлением главного
напряжения и плоскостью поляризации,
-
угол между направлением главного
напряжения и плоскостью поляризации, 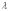 -
длина волны используемого света.
Если
=45°,
то (1.12) приобретает вид:
-
длина волны используемого света.
Если
=45°,
то (1.12) приобретает вид:
I
=I
sin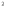
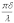 (9)
(9)
Таким образом, чтобы определить усилие в рельсе, достаточно измерить интенсивность света на выходе полярископа, и используя выражения (6) и (9) перейти к продольной силе, действующей в рельсовой плети.

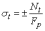
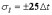 (кг/см2)
или
(кг/см2)
или 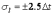 (МПа).
(МПа).