Статистическая группировка

Статистическая группировка – это метод исследования массовых общественных явлений путем выделения и ограничения однородных групп, через которые раскрываются существенные черты и особенности состояния и развития всей совокупности.

Виды группировок

(1) Типологические группировки

Их задача – выявление социально-экономических типов или однородных в существенном отношении групп.

№ п/п	Социально-экономические типы	Мужчины		Женщины
		1980	1992	1980	1992
1.	Работники	–	–	–	–
2.	Крестьяне	–	–	–	–
3.	Служащие	–	–	–	–

(2) Структурные группировки

Их задача – изучение состава отдельных типических групп при помощи объединения единиц совокупности, близких друг к другу по величине группировочного признака.

№ п/п	Количество посадочных мест	Количество столов	Число занятых	Товарооборот на 1 место
1.	до 25	–	–	–
2.	16 – 50	–	–	–
3.	51 – 70	–	–	–
4.	71 – 100	–	–	–

(3) Аналитические группировки

Их задача – выявления влияния одних признаков на другие ( выявить связь между социально-экономическими явлениями).

№ п/п	Группы магазинов по числу рабочих мест	Число магазинов	Товарооборот
			на 1 работника	на 1 раб. место
1.	до 5	100	12,0	13,0
2.	6 – 10	50	14,0	16,0
3.	11 – 15	10	15,0	17,0
4.	16 – 20	4	30,0	39,0
5.	21 – 25	2	31,0	42,0

(4) Комбинационные группировки

В них производится разделение совокупности на группы по двум или более признакам. При этом группы, образованные по одному признаку, разбиваются на подгруппы по другому признаку.

Такие группировки дают возможность изучить структуру совокупности по нескольким признакам одновременно.

№ п/п	Группы предприятий по объему основных фондов	Оплата труда в рублях	Пол	Количество единиц
1.	до 200	100 – 120	М	–
			Ж	–
		120 – 140	М	–
			Ж	–
		140 – 160	М	–
			Ж	–
2.	200 – 400	100 – 120	М	–
			Ж	–
		120 – 140	М	–
			Ж	–
		140 – 160	М	–
			Ж	–
3.	400 – 600	100 – 120	М	–
			Ж	–
		120 – 140	М	–
			Ж	–
		140 – 160	М	–
			Ж	–
4.	600 – 800	100 – 120	М	–
			Ж	–
		120 – 140	М	–
			Ж	–
		140 – 160	М	–
			Ж	–

Группировка по количественным признакам требует выбора размера интервала. Интервалы в статистических группировках — это те количественные значения признака, которые определяют величину отдельных групп совокупности. Интервалы в зависимости от размера могут быть равными, неравными и специализированными, а в зависимости от порядка построения верхней и нижней группы — открытыми и закрытыми. Равные интервалы применяются обычно при узких границах вариации признака, когда его распределение носит более или менее равномерный характер. Размер интервала, если данные сгруппированы определяется как разность между верхней и нижней границей группы (между максимальным и минимальным значением признака). В случае, если материал не сгруппирован, размер равновеликого интервала I определяется по формуле: значение группировочного признака в изучаемой совокупности; х - минимальное значение признака; n - число групп, на которые разбивается совокупность.

В большинстве случаев при исследовании экономических явлений используются неравные интервалы. Применение неравных интервалов обусловлено неодинаковым значением количественных изменений признака в низших и высших группах Специализированные интервалы применяются тогда, когда необходимо выделить группы, отличающиеся качественным своеобразием. Специализированными являются возрастные интервалы, отграничивающие различающиеся по трудоспособности группы населения. Границы специализированных интервалов не могут определяться произвольно. Каждый интервал отражает иное качество признака. Поэтому границы интервалов должны отражать переход из одного качества в другое. Интервалы могут быть открытыми и закрытыми. Открытыми называются интервалы, имеющие только одну границу (верхнюю или нижнюю). Закрытые интервалы имеют нижнюю и верхнюю границы.

9) Ряды распределения, их виды и графики. Схема вариационного ряда. Понятие признака, частоты (веса) признака, частности, кумулятивной частоты (частности).

В результате сводки и группировки статистических материалов получают ряды цифровых показателей, характеризующие отдельные стороны изучаемого явления. Эти ряды называются статистическими. По содержанию статистические ряды делятся наряды динамики и ряды распределения. Рядами распределения называются ряды, характеризующие распределение единиц совокупности по какому-либо признаку, разновидности которого расположены в определенном порядке. Ряды распределения бывают атрибутивными и вариационными. Атрибутивными называются ряды, образованные по атрибутивным признакам, например распределение населения по полу.

Построение атрибутивных рядов несложно: образуется столько групп, сколько вариантов атрибутивного признака имеет изучаемое явление.

Вариационные ряды распределения образуются по количественным признакам Вариационный ряд — это последовательность количественных значений признака, расположенных в порядке возрастания или убывания. В вариационном ряду различают два элемента: варианты и частоты. Варианта — это отдельное значение группировочного признака в вариационном ряду. Частоты — это числа, которые показывают, как часто встречаются те или иные варианты. Различают дискретные и интервальные вариационные ряды. Для дискретных рядов характерно прерывное изменение признака. Примером дискретного вариационного ряда является распределение семей по числу детей, где варианты — группы семей по числу детей, а частоты — число семей. В интервальных вариационных рядах значения вариант даются в виде интервалов. Вычисление статистических показателей в интервальном ряду возможно только при условии предварительного представления его в форме дискретного ряда, в котором вариантами являются средняя арифметическая величина нижней и верхней границ каждой группы.

Графическое изображение.

Ряды распределения удобно анализировать при помощи их графического

изображения, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда отражают полигон и гистограмма.

Полигон используется при изображении дискретных вариационных рядов.

Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные (упорядоченные) значения варьирующего признака, а по оси ординат наносится шкала для выражения частот. Пример построения полигона для данных таблицы 2 приведен на рисунке 1

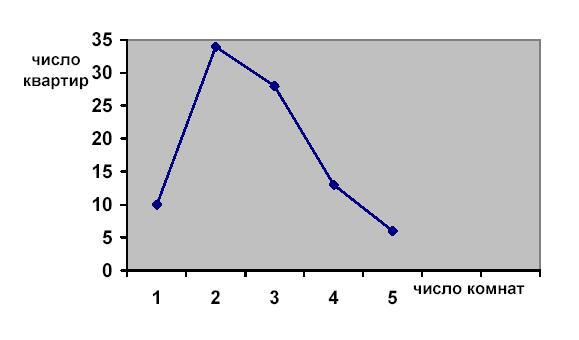Рисунок 1- Полигон распределения жилого фонда по типу квартир

Гистограмма применяется для изображения интервального ряда. При

построении гистограммы на оси абсцисс откладываются величины интервалов,

а частоты изображаются прямоугольниками, построенными на соответствую-

щих интервалах. Высота столбиков в случае равных интервалов должна быть

пропорциональна частотам.

Пример построения гистограммы для данных, приведенных в таблице 3,

показан на рисунке 2 .

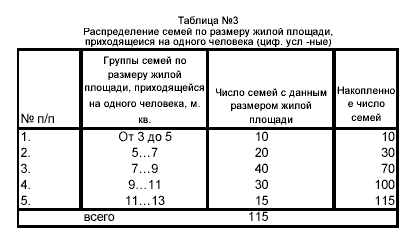
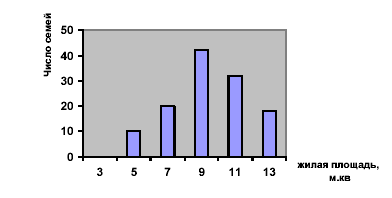
Рисунок 2 - Гистограмма распределения семей по размеру жилой площади,

При построении гистограммы распределения вариационного ряда с нерав-

ными интервалами по оси ординат следует наносить не частоты, а плотность

распределения признака в соответствующих интервалах..

Для графического изображения вариационных рядов может также ис-

пользоваться кумулятивная кривая (кривая сумм). При помощи кумуляты

изображается ряд накопленных частот. Накопленные частоты определяются

путем последовательного суммирования частот по группам.

При построении кумуляты по оси абсцисс откладываются варианты ряда,

а по оси ординат накопленные частоты. Пример построения кумуляты для

данных, приведенных в таблице 3 показан на рисунке 3 .

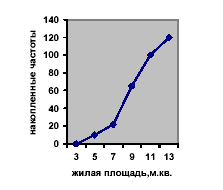
Рисунок 3- Кумулята распределения семей по размеру жилой площади,

приходящейся на одного человека

Если при графическом изображении вариационного ряда в виде кумуляты

координатные оси поменять местами, то полученное изображение называют

огивой

Признак – это характерное свойство изучаемого явления, отличающего

его от других явлений.

В разных отраслях статистики изучаются разные признаки так например

объектом изучения является предприятие, а его признаком, вид

продукции . Или объект отдельный человек, его признаки (рост, вес и

т.д.).

10) абсолютные статистические величины и их виды.