47. Средние индексы:среднеарифмитический и среднегармонический.

Средние индексы могут быть получены путем преобразования агрегатных индексов и индивидуальных.

Существует два вида средних индексов:

1. Средний арифметический индекс;

2. Средний гармонический индекс;

Средний арифметический индекс применяется в тех случаях, когда известно готовое произведение (выручка от реализации продукции) только базисного периода, а также изменение индивидуального индекса. Все преобразования будут производится в числителе агрегатного индекса. Среднеарифметический индекс цен.

Среднегармонический индекс применяется в тех случаях, когда известно готовое произведение отчетного периода или отчетного и базисного периода одновременно, а также изменение индивидуального индекса. Преобразования производятся в знаменателе агрегатного индекса.Среднегармонический индекс цен.

Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности. Среднеарифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей.

Среднегармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс себестоимости можно исчислить так:

Таким образом, весами при определении среднегармонического индекса себестоимости являются издержки производства текущего периода, а при расчете индекса цен стоимость продукции этого периода.

48. Индексы средних величин и их взаимосвязь: индекс переменного состава, индес постоянного состава и структурных сдвигов.

На динамику качественных показателей, уровни которых выражены средними величинами, оказывает влияние изменение структуры изучаемого явления. Под изменением структуры явле­ния здесь понимают изменение доли отдельных единиц сово­купности, из которых формируются средние, в общей их чис­ленности.

Структурные сдвиги в экономике — это важные процессы со­вершенствования производства и большой дополнительный ис­точник развития производительных сил общества. В связи с этим при анализе развития экономики страны важно определить, в ка­кой мере это развитие зависит от структурных сдвигов, т.е. какой экономический эффект дает то или иное улучшение структуры производства (в разных масштабах, на различных участках).

Таким образом, при изучении динамики средней величины задача состоит в определении степени влияния двух факторов — изменений значений осредняемого показателя и изме­нений структуры явления. Эта задача решается с помощью ин­дексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигав.

• Изучение совместного действия этих двух факторов на общую динамику среднего уровня осуществляется в статистике с помощью индекса переменного состава. Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами, показывающее изменение индексируемой средней величины.

Для любых качественных показателей индекс переменного состава можно записать в общем виде: , где - уровни осредняемого показателя в отчетном и базисном периодах соответственно, - веса (частоты) осредняемого показателя в отчетном и базисном периодах соответственно.

• Чтобы элиминировать влияние изменения структуры со­вокупности на динамику средней величины, берут отношение средних взвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс, характеризующий дина­мику средней величины при одной и той же фиксированной структуре совокупности, носит название индекса постоянного (фиксированного) состава и исчисляется в общем виде:

.

• Для измерения влияния только структурных изменений исследуемый средний показатель исчисляют индекс структур-сдвигов, как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структу­ру, к фактической средней этого показателя в базисном периоде:

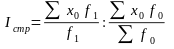
В качестве весов (частот) индексов средних величин, наряду с абсолютными показателями f могут использоваться и относи­тельные показатели (частоты, доли) d. В последнем случае упомянутые индексы для любых качественных показателей х можно выразить в общем виде следующими формулами: ; ; , где доли единиц с определенным значением признака в общей совокупности в отчетном и базисном периодах соответственно ( )

ВЗАИМОСВЯЗЬ ИНДЕКСОВ

Между важнейшими индексами существуют взаимосвязи, позволяющие на основе бЙйМк индексов получить другие. Зная, например, значение цепных индексов за какой-либо период вре­мени, можно рассчитать базисные индексы. И наоборот, если известны базисные индексы, то путем деления одного из них на другой можно получить цепные индексы.

Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например связь между индексом стоимос­ти продукции, физического объема продукции и цен (п. 12.7). Другие индексы также связаны между собой. Так, индекс из­держек производства - это произведение индекса себестоимо­сти продукции и индекса физического объема продукции:

(12.42) или

Индекс затрат времени на производство продукции может быть (получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемко­сти, т, е. индекс производительности труда

или

■ ■•

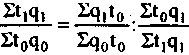При увеличении физического объема продукции в текущем периоде на 15% по сравнению с базисным производительность понизилась на 18%, поэтому индекс затрат времени на производ­ство продукции^будет равен:

1,15 : 0,82 = 1,402, или 140,2%.

Существует важная взаимосвязь между индексами физичес-коro объема продукции и индексами производительности труда. Индекс производительности труда рассчитывается на основе следующей формулы:

'

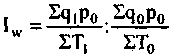т. е. представляет собой отношение средней выработки продук-ции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах. Индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат "рабочего времени (или численности занятых):

.

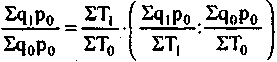
Взаимосвязь между отделными индексами может быть использована для выявления влияния отдельных факторов, оказывающих воздействие на изучаемое явление.