2.2.2. Планирование товарооборота

Коммерческое предприятие реализует товары нескольких групп: . Для реализации этих товаров используются ресурсы с ограниченным объемом: — рабочее время (чел.-ч); -площадь залов ( ); - издержки обращения (руб.). Известны нормы расхода каждого вида ресурса на реализацию единицы j-й группы товара — . Доход от продажи в расчете на единицу товара составляет .

Необходимо составить оптимальный план товарооборота по критерию максимума дохода (или по другому критерию — минимум издержек обращения).

Построение экономико-математической модели задачи

Известно, что величина дохода линейно связана с объемом продажи товаров . В связи с этим целевую функцию можно записать в виде

.

Очевидно, что объем продажи товаров не может быть отрицательной величиной. Поэтому .

Учитывая нормы затрат ресурсов и их объемы, запишем ограничения в виде системы:

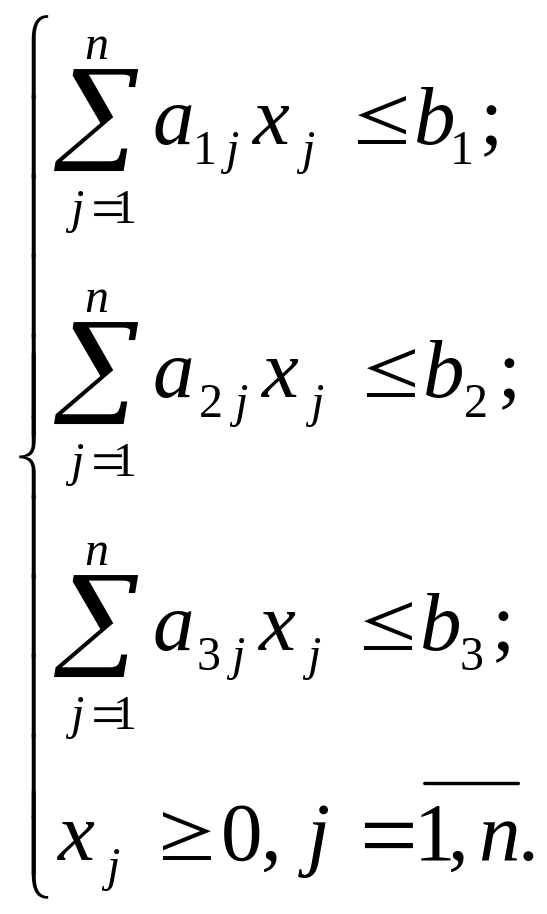
Решение задачи можно получить с помощью симплексного метода, рассмотренного ниже в п. 2.3.2.

2.2.3. Производственная задача

Предприятие изготавливает несколько видов продукции, расходуя на это изготовление различные виды сырья. Запасы сырья ограничены. Доход, получаемый от реализации каждого вида продукции, различен. Необходимо составить такой план выпуска продукции, при котором доход предприятия был бы максимальным.

Для изготовления n видов продукции используется m видов сырья .

Запасы сырья составляют . Нормативы затрат сырья на изготовление единицы продукции составляют . Доход, получаемый от реализации единицы продукции j-го вида, составляет .

Необходимо составить такой план выпуска продукции, при котором доход от ее реализации будет максимальным.

Построение экономико-математической модели задачи.

Обозначим количество единиц продукции j-го вида , запланированных к производству. Тогда целевая функция будет иметь вид:

Для изготовления всей продукции потребуется единиц сырья i-го вида. Поскольку его количество ограничено величиной , получаем неравенство

Учитывая нормативы затрат и ограничения на ресурсы, запишем систему неравенств:

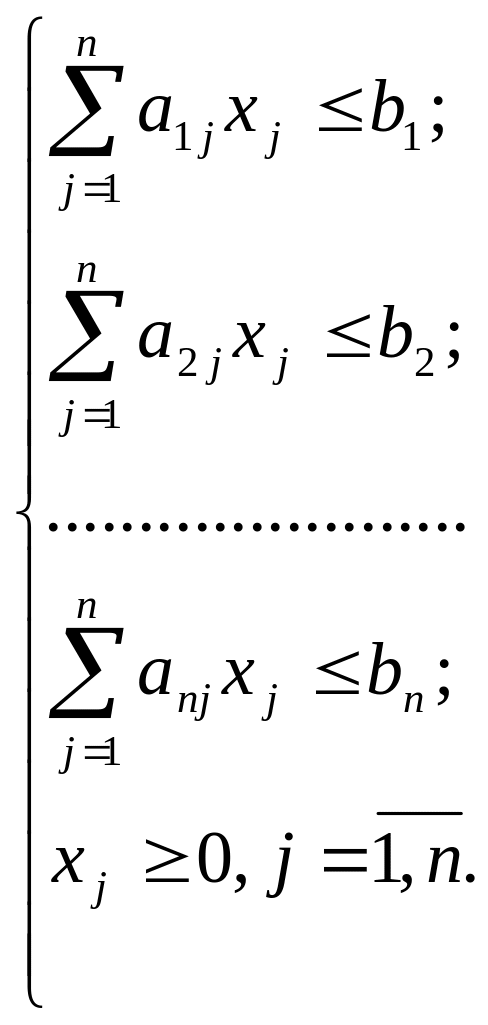
Рассмотрим примеры построения экономико-математических моделей.

Пример 1.

Построить экономико-математическую модель определения структуры выпуска первых и вторых блюд предприятия общественного питания при заданном квартальном плане товарооборота 270 тыс. руб. и получении максимального дохода на основе данных, приведенных в таблице 2.2.2.

Таблица 2.2.2

Ресурсы	Плановый фонд ресурсов	Нормативные затраты ресурсов на 100 блюд
		1-е блюда	2-е мясные	2-е рыбные	2-е Молоч- ные	2-е Про-чие
Затраты труда на производст-во, чел.-ч	78 000	3,4	5,0	38,0	2,6	23
Затраты труда на обслужива-ние, чел.-ч	130 000	2,1	5,2	5,1	2,8	3
Издержки производст-ва и обращения, руб.	16 300	4,3	6,9	6,7	26	4,1
Доход, руб.		1,3	2,0	1,5	0,3	1,7
Товарообо-рот, руб.	270 000	25	37	23	22	20

Экономико-математическая модель задачи имеет следующий вид.

Найти такое количество выпускаемых блюд, — вектор которое при заданных ограничениях по использованию ресурсов, представленных в виде системы линейных неравенств

обеспечивает максимум дохода в соответствии с целевой функцией вида

Пример 2.

Построить экономико-математическую модель определения структуры выпуска блюд на предприятии общественного питания, обеспечивающую максимальный доход на основе заданных объемов, ресурсов и нормативов затрат продуктов на первые и вторые блюда, представленных в таблице 2.2.3.

Таблица 2.2.3

Ресурсы	Плано-вый фонд ресур-сов	Нормативные затраты ресурсов на 100 блюд
		1-е блюда	2-е мясные	2-е рыбные	2-е молочные	2-е прочие
Мясо, кг	40 000	4,0	8,0	-	-	3,8
Рыба, кг	25 000	2,5	-	10	-	-
Овощи, кг	27 000	3,2	2,0	3,0	-	4,6
Мука, крупа, кг	20 000	2,1	2,6	2,3	-	2,8
Молоко, л	50 000	6,5	-	-	21	-
Доход, руб.		1,3	2,0	1,5	0,3	1,7

Экономико-математическая модель задачи имеет следующий вид.

Найти такое количество выпускаемых блюд, – арифметический вектор, который при заданных ограничениях

обеспечивает максимум дохода в соответствии с целевой функцией