Глава 2. Методы и модели линейного программирования

Постановка задачи коммерческой деятельности может быть представлена в виде математической модели линейного программирования, если целевая функция может быть представлена в виде линейной формы, а связь с ограниченными ресурсами описывается посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение — значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и

другие экономические показатели. В целом экономико-математическая формулировка и модель общей задачи линейного программирования (ОЗЛП) имеют следующий вид:

найти максимальное (минимальное) значение линейной целевой функции

(1)

при условиях-ограничениях:

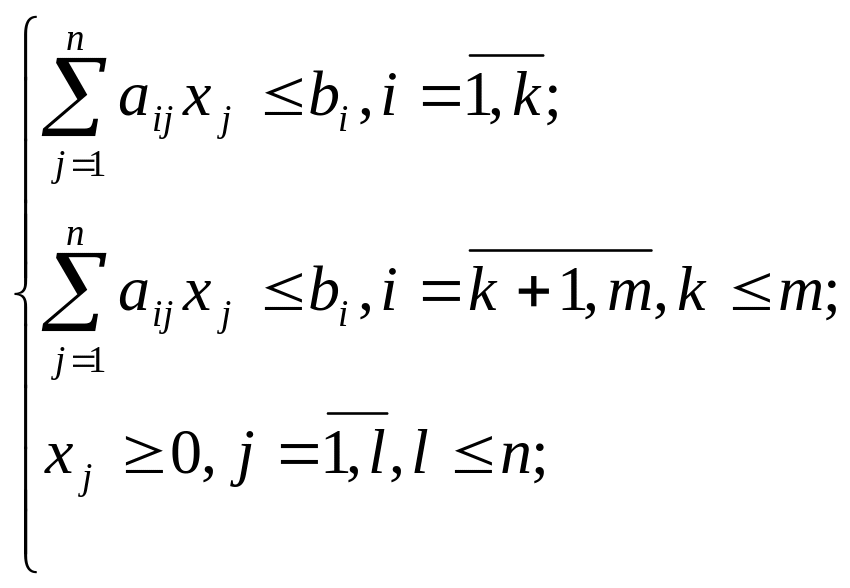(2)

где — заданные постоянные величины.

2.1. Общая задача линейного программирования

Стандартной задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения целевой функции (1) при выполнении условия первого из системы (2) — нетривиального и условия третьего из системы (2) — тривиального.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения целевой функции (1) при выполнении второго и третьего условий из системы (2).

Для перехода от стандартной формы записи задачи линейного программирования к канонической необходимо ограничение - неравенство исходной задачи линейного программирования, имеющее вид « », преобразуется в ограничение — равенство с добавлением к левой части дополнительной неотрицательной переменной. Ограничение — неравенство вида « » преобразуется в ограничение — равенство вычитанием из левой части дополнительной неотрицательной переменной.

В системе из m линейных уравнений с n переменными базисными (основными) называются любые m переменные, если соответствующий им определитель матрицы коэффициентов отличен от нуля, а остальные (n-m) переменные называются свободными.

В базисном решении все (n-m) свободные переменные равны нулю.

Допустимое базисное решение (опорный план) содержит только неотрицательные переменные, среди которых свободные равны нулю.

Допустимое базисное решение является невырожденным, если все базисные переменные строго положительны, и вырожденным — в противном случае.

Оптимальное решение задачи линейного программирования совпадает с одним из ее допустимых базисных решений.

Совокупность чисел , удовлетворяющих тривиальным и нетривиальным ограничениям задачи, называется допустимым решением (или в экономических задачах — планом).

Совокупность допустимых решений формирует область допустимых решений (ОДР).

План , при котором целевая функция задачи принимает экстремальное значение, называется оптимальным.

В случае, когда требуется найти минимум функции

можно перейти к нахождению максимума функции

так как

тогда полученное решение целевой функции следует записать с обратным знаком.