2.2.6. Задача о назначениях

В коммерческой сфере возникают задачи, связанные с необходимостью выбора такого варианта распределения ресурсов: трудовых, товарных, финансовых, энергетических, материальных, природных и других по некоторым объектам -магазинам, городам, предприятиям, цехам и т.п., который обеспечил бы минимальные

затраты денег, времени или максимальные прибыль и доход и минимальные издержки.

Так, например, всегда актуальной является проблема формирования трудового коллектива.

Известно, что один и тот же работник может выполнять различные функции с разной производительностью в зависимости от опыта работы, квалификации, индивидуальных особенностей. Поэтому возникает задача о назначениях, предполагающая такое распределение работников по должностям, при котором производительность труда в коллективе была бы максимальной.

Построение экономико-математической модели задачи.

На коммерческом предприятии имеется m работников: , каждый из которых должен выполнять одну из имеющихся n видов работ: .

Для каждого работника на рабочем месте рассчитывается производительность труда . Необходимо определить, кого и на какую работу следует назначить, чтобы добиться максимальной или минимальной стоимости назначения суммарной производительности при условии, что каждый работник может быть назначен

только на одну работу.

Обозначим назначение i-го работника на j-ю работу. Количество работников m равно количеству работ, поэтому может принимать только два целочисленных значения: 1, если i-й работник назначен на выполнение j-й работы; О, если не назначен.

При назначении i-го работника на j-ю работу производительность или стоимость назначения равна . Необходимо построить квадратную матрицу распределения по должностям X, которая обеспечивает максимальное или минимальное значение линейной функции цели

при ограничениях

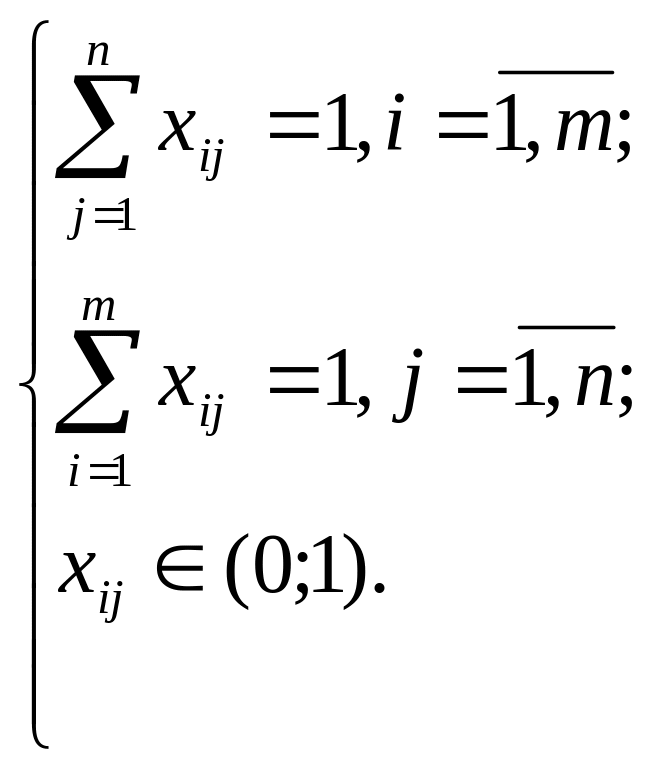
Задача о назначениях является частным случаем транспортной задачи, поэтому для ее решения можно воспользоваться любым алгоритмом линейного программирования, однако более эффективным является венгерский метод.

2.2.7. Формирование торговой сети

В регионе расположены населенные пункты, численность жителей которых, а также расстояние между ними, стоимость поездок известны. Кроме того, задано множество типовых проектов предприятий общественного питания. Необходимо найти оптимальный план размещения предприятий общественного питания в регионе, обеспечивающий минимальные приведенные затраты на их строительство, эксплуатацию и на поездки населения между населенными пунктами.

Построение экономико-математической модели задачи.

Введем обозначения показателей, которые относятся к содержанию задачи:

n - количество населенных пунктов;

j— номер населенного пункта; ;

- численность населения j-го населенного пункта;

- расстояние между пунктами i и j;

i — индекс пункта размещения предприятия общественного питания ( );

— количество типовых вариантов предприятий для j-го пункта;

q — номер типового предприятия общественного питания ;

— спрос населения в j-м населенном пункте на продукцию общественного питания;

b — норма обеспеченности продукцией общественного питания одного человека;

— максимально допустимый радиус передвижения населения;

— численность населения j-го пункта, обслуживаемого предприятием i-го пункта;

— типовой вариант q предприятия общественного питания i-го пункта;

— текущие затраты для ;

— единовременные затраты для ;

— затраты на поездку одного жителя из пункта i в пункт j;

— нормативный коэффициент эффективности капитальных вложений.

В качестве критерия оптимальности принимаем приведенные затраты С на строительство, эксплуатацию и на поездки населения. Тогда формальная запись задачи представляет такой вид: найти такие типовые варианты предприятий общественного питания для каждого i-го пункта и численности населения j-го пункта, обслуживаемого предприятиями i-го пункта, обеспечивающие минимум затрат в соответствии с целевой функцией вида

при следующих условиях-ограничениях: предложение продукции общественного питания, предоставляемое населению района предприятиями общественного питания j-го пункта, должно соответствовать мощности предприятия:

;

потребность населения j-го пункта в продукции, обеспечиваемой предприятиями района, должна быть удовлетворена:

;

расстояние от j-го пункта расселения до i-го пункта размещения предприятия не должно превышать допустимого радиуса обслуживания . Кроме того, существуют ограничения на переменные .

Решение этой задачи проводят путем последовательного подбора типовых мощностей предприятий торговли или общественного питания в модели и определении величин затрат для каждого варианта.