2.2.5. Перевозка грузов

В современных условиях большие транспортные расходы связаны с простоями в ожидании обслуживания на погрузочно-разгрузочных работах, порожними пробегами, встречными и нерациональными перевозками, затратами на бензин, техническое обслуживание и заработную плату водителей. В связи с этим необходимо решать задачи оптимального планирования перевозок грузов в коммерческой деятельности из пунктов отправления (баз, станций, фабрик, совхозов, заводов) в пункты назначения (магазины, склады) методами, позволяющими оптимизировать план по какому-либо экономическому показателю, например финансовых затрат или времени на перевозку грузов.

Для решения подобного рода задач в линейном программировании существуют специально разработанные методы, а задачи такого рода называются транспортными задачами.

Построение экономико-математической модели задачи

Имеется m пунктов отправления (поставщиков) грузов: , на которых сосредоточены запасы какого-либо однородного груза в объемах соответственно: .

Величины определяют максимально возможные размеры вывоза груза с пунктов отправления. Суммарный запас груза поставщиков составляет . Кроме того, имеется n пунктов назначения: , которые подали заявки на поставку грузов в объемах соответственно: .

Суммарная величина заявок составляет . Стоимость перевозки одной единицы груза от поставщика к потребителю обозначим через (транспортный тариф), образующих матрицу транспортных издержек С. В качестве критерия оптимальности выбираем суммарные издержки по перевозке грузов.

Тогда транспортная задача формулируется следующим образом: необходимо составить оптимальный план, т.е. найти такие значения объема перевозок грузов от поставщиков к потребителям , чтобы вывести все грузы от поставщиков; удовлетворить заявки каждого потребителя и обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные транспортной задачи можно записать в виде таблице 2.2.5, которая называется транспортной: С и Х.

Задача заключается в определении плана перевозок – матрицы , которая удовлетворяет следующим условиям:

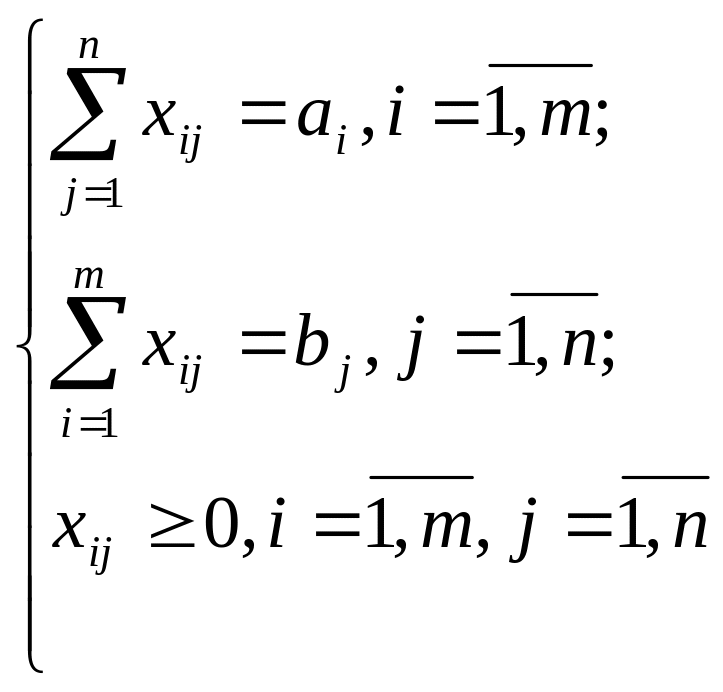
Таблица 2.2.5

Пункты отправления	Пункты назначения						Запасы
			…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
Заявки			…		…

и обеспечивает минимальное значение целевой функции

в таком виде экономико-математическая постановка транспортной задачи считается законченной, а ее решение изложено ниже в разделе 2.7.

Транспортная задача может быть решена на компьютере, поскольку математические методы, как правило, реализованы в виде специальных программ.