Это означает, что интервал любой прямой, лежащей в плоскости, больше интервала масштаба уклона или равен ему.

Рассмотрим случаи, когда требуется в заданной плоскости провести прямую с заданным уклоном и через данную прямую провести плоскость с заданным уклоном.

Пусть через точку А₇, лежащую в плоскости Σi (рисунок 16) требуется провести прямую с заданным уклоном i = 1:2. Для этого из точки А как из центра проведем окружность с радиусом R, равным интервалу прямой заданного уклона.

i = 1:2. = 2 R = 2 ед

В пересечении ее с соседними горизонталями обозначим КМ и NL. Прямые MN и KL , проходящие через точку А, лежат в плоскости Σ и имеют заданный уклон. Задача имеет два решения.

На рисунке 17 Решена обратная задача: через прямую АВ проведены плоскости Σ и Ω с заданным уклоном (задача тоже имеет два решения)

i = 1:2

=2

Горизонтали плоскости с целочисленными отметками должны проходить через точки прямой, имеющие так же отметки и проекции этих горизонталей должны быть расположены на расстояниях, равных интервалу масштаба уклонов плоскости.

Для решения задачи выполняем следующие построения. Из точки, лежащей на прямой и имеющей целочисленную отметку, например, из точки 4, как из центра опишем дугу окружности с радиусом R , равным заданному интервалу масштаба уклона плоскости.

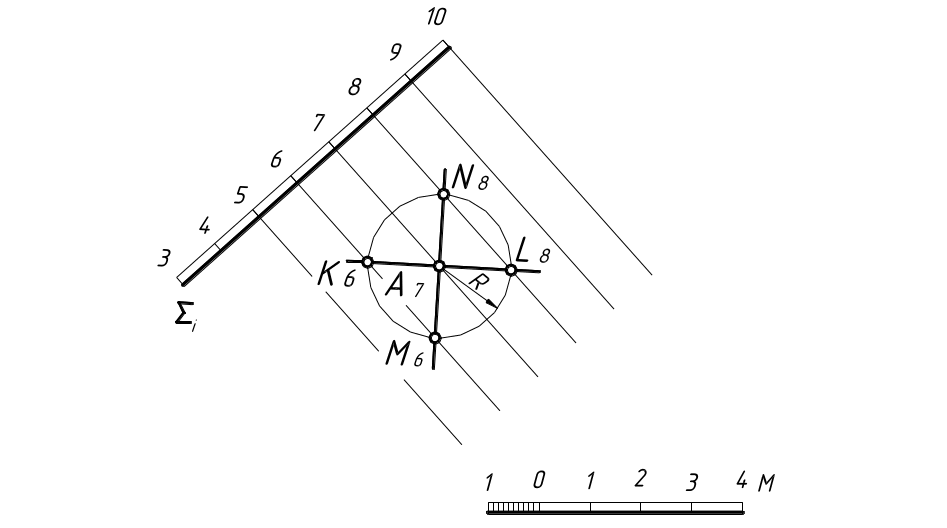
Рисунок 16

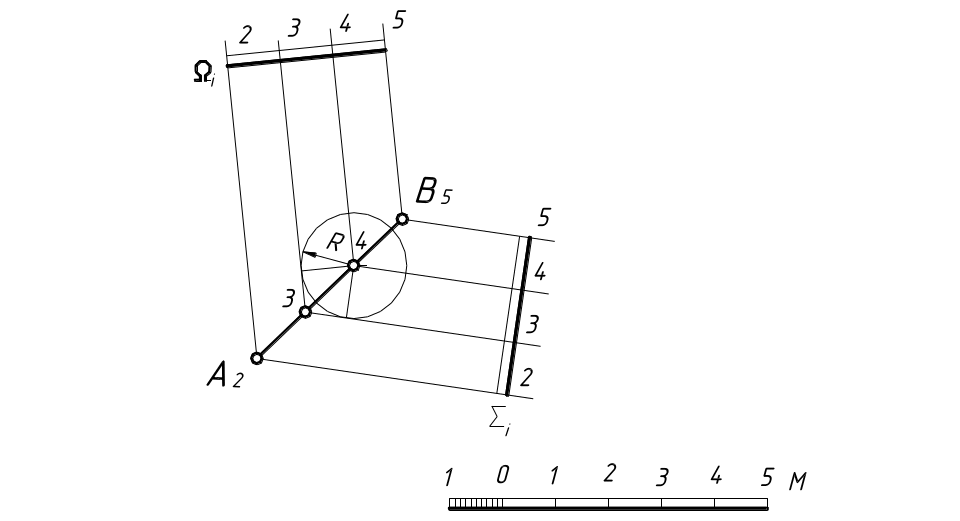
Рисунок 17

Из соседней точки с отметкой 3 проводим касательные к окружности, которые будут являться горизонталями плоскостей Σ и Ω . Остальные горизонтали плоскости проходят параллельно полученным через точки прямой, имеющие целочисленные отметки.

Масштабы уклонов плоскостей перпендикулярны горизонталям.

3.2. Проекции многогранников

Применяя метод проекций с числовыми отметками для изображения геометрических тел, необходимо на проекции данного тела указывать отметки характерных точек и линий.

В многограннике характерными точками являются его вершины.

На рисунке 16 дана проекция S, A, B, C пирамиды SABC, основание которой расположено в плоскости П_о , а вершина отстоит от нее на 3 м.

Рисунок 18 Рисунок19

3.3. Проекции кривых поверхностей

Если задана кривая поверхность, то для ее изображения в проекциях с числовыми отметками прибегают к горизонталям, представляющим собой линии пересечения поверхности плоскостями, параллельными П₀ и отстоящими друг от друга на единицу высоты.

На рисунке 19 изображен прямой круговой конус, стоящий основанием на плоскости П₀ . Проекцией конуса являются концентрические окружности с числовыми отметками.

Кривые поверхности в проекциях с числовыми отметками задаются проекциями их горизонталей с числовыми отметками.

Такой способ задания поверхности является наиболее удобным для изображения неправильных поверхностей, так называемых графических или в применении к земной поверхности – топографических. По отметкам горизонталей можно судить о форме изображенной поверхности.

Рисунок 20

Так, на рисунке 20 изображена котловина, низшая горизонталь которой имеет отметку 7.

3.4. Поверхность одинакового ската

Поверхностью одинакового ската называется линейчатая

поверхность, все прямолинейные образующие которой составляют с плоскостью одинаковый угол.

Если прямой круговой конус перемещать так, чтобы его вершина скользила по некоторой направляющей MN , а его ось оставалось перпендикулярной к горизонтальной плоскости, то поверхность, обвертывающая различные положения конуса, будет являться поверхностью одинакового ската (рисунок 21).

Рисунок 21

Если на поверхности одинакового ската провести горизонтали этой поверхности, то они будут касаться соответствующих сечений круговых конусов, расположенных на определенных отметках.

На рисунке 22 показано построение горизонталей поверхности одинакового ската в проекциях с числовыми отметками.

Поверхности откосов, насыпей и выемок криволинейных участков дорог на подъемах и спусках представляют собой поверхности одинакового ската.

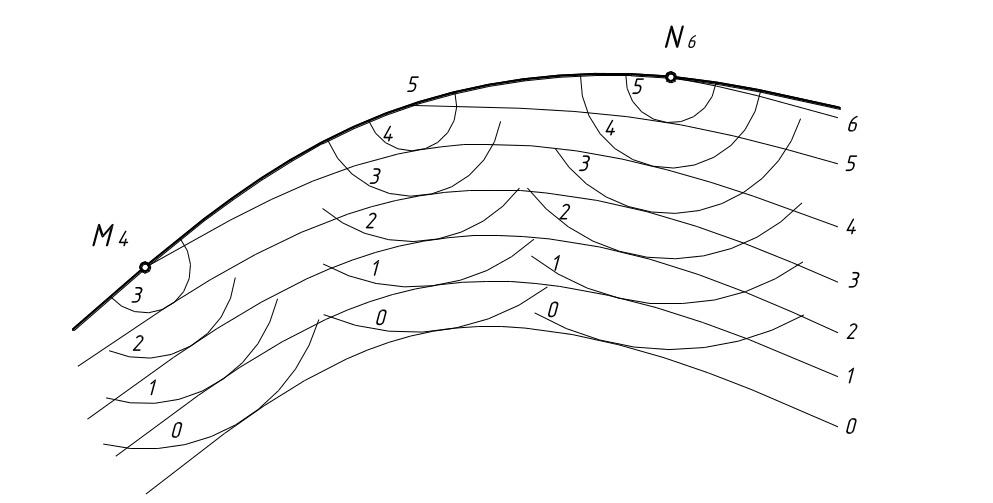
Рисунок 22