Государственное образовательное учреждение

Высшего профессионального образования

«Камская государственная инженерно-экономическая академия»

Проекции с числовыми отметками

Методические указания к выполнению задания по начертательной

геометрии и черчению

Набережные Челны

2006

УДК 121.021.(076)

Проекции с числовыми отметками: Методические указания к практическим занятиям по начертательной геометрии / Составители Ахмедова А.А., Рзаева Т.В., Шарафутдинова Р.В.– Наб. Челны: ИНЭКА, 2006. – 24 с.

Печатается в соответствии с решением научно-методического совета Камской государственной инженерно-экономической академии.

Методические указания предназначены в помощь студентам заочного отделения инженерно-строительного факультета. Включает краткое изложение теории по теме «Проекции с числовыми отметками» и необходимый материал для выполнения задания.

Рецензент: к.т.н., доцент кафедры СК Ш.Х. Нетфулов

Проекции с числовыми отметками

1. Сущность метода. Проекции точек

Метод проекций с числовыми отметками находит широкое применение в тех случаях, когда высота изображаемого предмета невелика сравнительно с его длиной и шириной и при изображении поверхности земли.

Сущность метода заключается в том, что предмет проецируется методом ортогонального проецирования только на одну плоскость проекций, которая располагается горизонтально, называется плоскостью нулевого уровня и обозначается П₀.

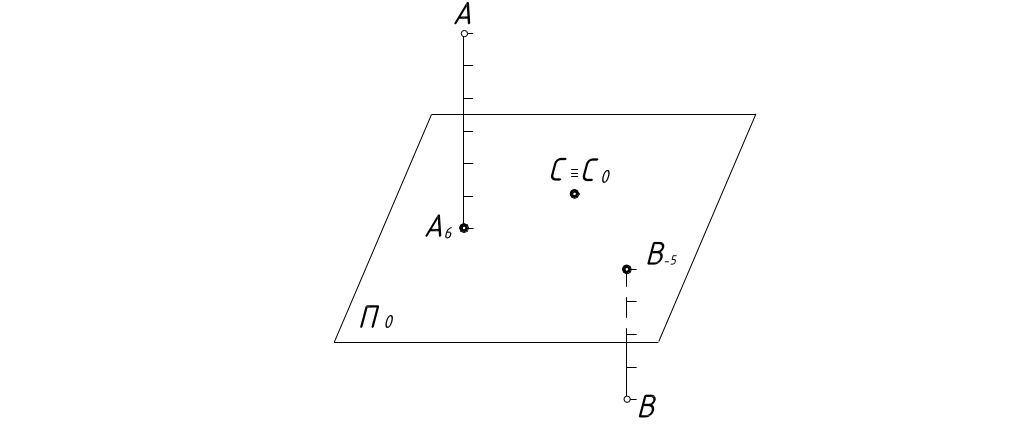
Чтобы по чертежу иметь возможность восстановить положение точки в пространстве, рядом с проекцией каждой точки проставляется цифра – числовая отметка, указывающая в метрах расстояние от точки до плоскости нулевого уровня.

Точки, расположенные над плоскостью нулевого уровня, имеют положительные отметки, точки, расположенные ниже плоскости, имеют отрицательные отметки, точки, лежащие в плоскости, имеют нулевую отметку.

Рисунок 1

На рисунке 1 наглядно показано построение проекций точек. Числовые отметки, проставленные у точек А, В, С показывают, что точка А находится над плоскостью П₀ на высоте 6 м. Точка В расположена под плоскостью П₀ на расстоянии 5 м. А точка С лежит в плоскости нулевого уровня.

Рисунок 2

Изображение этих трех точек в проекциях с числовыми отметками дано на рисунке 2.

Обычно расстояние точек от плоскости нулевого уровня выражается в тех же единицах масштаба, в которых измеряются расстояния на этой плоскости.

2. Проекции прямых линий

Прямая линия в проекциях с числовыми отметками изображается проекцией на П₀ и отметками двух точек.

Условимся называть длину проекции отрезка прямой заложением прямой и обозначать L ( см. рисунок 3).

Разность высот концов отрезка назовем превышением и обозначим J

h_B – h_A =J

Рисунок 3

Заложение прямой, соответствующее единице превышения, называется интервалом прямой и обозначается .

Интервал численно равен отношению заложения к превышению

;

Величина превышения, приходящаяся на заложение, равной единице называется уклоном i .

;

где - есть угол наклона прямой к плоскости.

Проградуировав проекцию прямой, можно графически определить интервал прямой.

Проградуировать проекцию прямой – значит определить на ней точки с постоянной разностью отметок, равной единице.

На рисунке 4 показано графическое градуирование проекции отрезка АВ методом пропорционального деления.

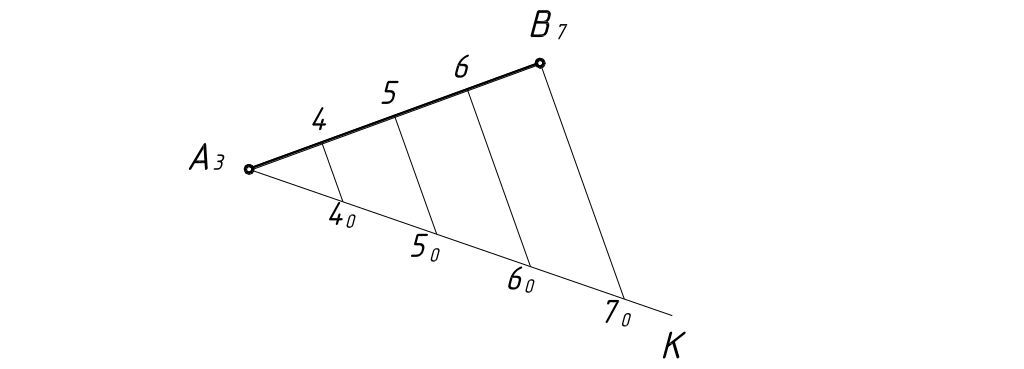
Рисунок 4

Через точку А произвольно проведен отрезок прямой АК, на котором отложены произвольные равные отрезки А₃ 4₀ , 4₀ 5₀ , 5₀ 6₀ , 6₀ 7₀.

Прямые, проведенные из точек 4₀ , 5₀ ,6₀ параллельно прямой 7₀ В определяют в пересечении с проекцией прямой искомые точки 4, 5, 6.

Г оризонтальная прямая проецируется на плоскость нулевого уровня в прямую, имеющую одинаковые числовые отметки двух точек рисунок 5 (рисунок 5).

Вертикальная прямая проецируется на плоскость нулевого

уровня в точку, имеющую числовые отметки двух точек (рисунок 5).