1. Оптическим волноводом называется направляющая структура, обеспечивающая распространение оптического излучения вдоль нее. Простейшим оптическим волноводом является планарный волновод. Он представляет диэлектрическую структуру (рис.5.1), состоящую из тонкого оптически прозрачного слоя с показателем преломления n₁ и прозрачной подложки с показателем преломления n₂, причем n₁  n₂. Выше слоя с n₁ может находиться свободная среда, например воздух с n₀, что соответствует несимметричному волноводу, или аналогичная подложке среда c n₂ . В этом случае образуется симметричный планарный волновод.

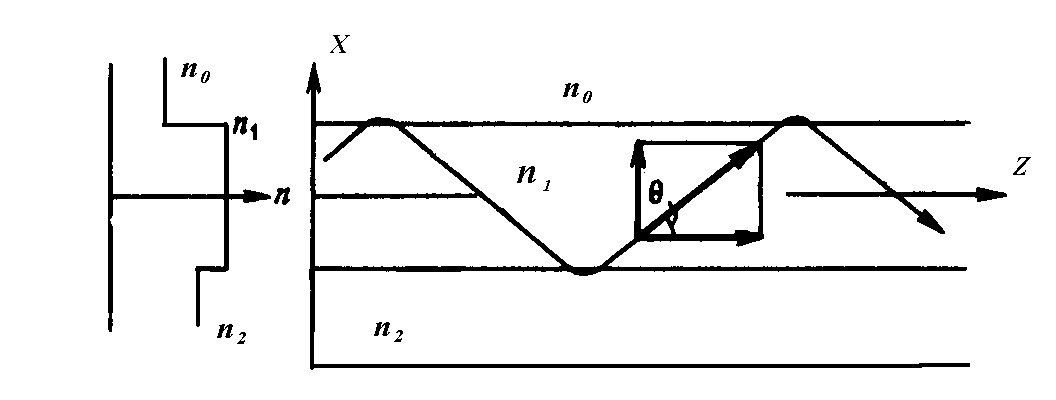
Рис.5.1. Планарный оптический волновод.

Максимальный угол ₁ , при котором происходит это явление, называется критическим углом и определяется соотношением

_пад = _кр = arccos (n₂ /n₁) .

2n₁khsin_m - 2₁₀ - 2₁₂ = 2m-ур-е планарного опт волновода.

оптическое волокно (ОВ), которое представляет собой оптический волноводный слой круглого сечения с показателем преломления n₁, окруженный однородной средой с меньшим показателем преломления n₂ (рис.5.5). Волноводный слой обычно называют сердцевиной волокна, а окружающую среду с показателем n₂–оболочкой волокна. Основным материалом, из которого изготавливаются сердцевина и оболочка оптических волокон, является высокочистое кварцевое стекло. Оболочка сверху покрыта защитным слоем, которое обычно выполняется из синтетических материалов и наносится на оболочку с целью защиты ОВ от внешних воздействий

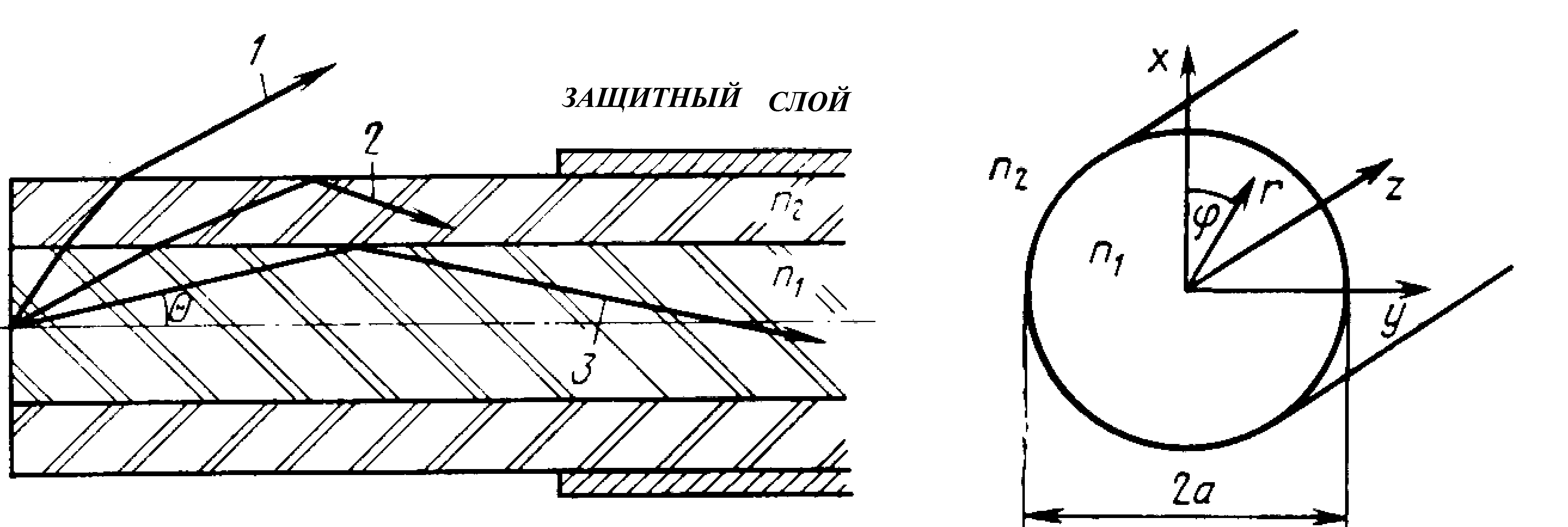
2. В случае слабонаправляющего оптического волокна, когда показатель преломления оболочки n₂ незначительно меньше показателя преломления сердцевины n₁, или n₁ – n₂  n₁. При выполнении этого условия направляемые моды распространяются под очень малыми углами . Их можно считать плоскими оптическими волнами, распространяющимися в направлении z, а их поля практически поперечны.

В пространстве, свободном от источников и заполненным однородной средой с магнитной проницаемостью  = ₀ и диэлектрической проницаемостью  = ₀, справедливо получаемое из уравнений Максвелла однородное волновое уравнение для вектора электрического поля

E + k²E = 0. (5.6)

Для поперечного электрического поля решение волнового уравнения (5.6) в цилиндрических координатах r, Ф, z (рис.5.5, б ) можно представить в виде

- в сердцевине;

(5.7)

- в оболочке,

где J_m функция Бесселя первого рода целочисленного порядка m; K_m - модифицированная Бесселя (функция Ганкеля) того же порядка.

При этом параметры U и R в (5.7) оказываются связанными с волновыми числами k₁ и k₂ материалов и постоянной распространения  следующим образом:

U² = a²(k₁² -²), R² = a²(² – k₂²) (5.8)

Решением (5.7) принимаем, что электрическое поперечное поле во всем сечении линейно поляризовано и одинаково в направлении x. В соответствии с уравнениями Максвелла этому поперечному электрическому полю соответствует следующее поперечное магнитное поле:

- в сердцевине,

(5.9)

- в оболочке,

где - волновое сопротивление материала сердцевины и оболочки. Аксиальные компоненты поля малы по сравнению с соответствующими поперечными компонентами благодаря малым углам наклона . Поэтому ими можно пренебречь и простое соотношение (5.9) для поперечных полей справедливо. При этом поперечное магнитное поле перпендикулярно поперечному электрическому, а отношение их величин такое же, как и в однородной плоской волне в такой же среде.

Соотношения (5.7), (5.9) удовлетворяют уравнениям Максвелла в приближении малого угла  или, что эквивалентно, малых аксиальных полей. Необходимо только обеспечить непрерывность тангенциальных компонентов поля Е_z и Н_z на границе сердечника и оболочки при r=а. Эти граничные условия удовлетворяются приведенными выражениями для электромагнитного поля при n₁  n₂, если выполняется равенство

. (5.10)

Соотношение (5.10) является упрощенным характеристическим уравнением для однородных и линейно-поляризованных волн сердцевины в слабонаправляющем оптическом волокне при n₁  n₂. Оно определяет пару значений U и R, которые описывают в (5.7)и (5.9) поперечное распределение поля волн сердечника, причем U/а является радиальным волновым числом в сердцевине, а R/а - радиальным коэффициентом затухания в оболочке. С помощью (5.8) можно найти важный параметр оптического волокна, называемый нормированной частотой V, который определяется как

(5.11)

Используя последнее соотношение можно быстро и достаточно точно определить является оптическое волокно одномодовым или многомодовым, а также количество мод, поддерживаемое волокном.

3.

По количеству распространяющихся мод оптические волокна делятся на одномодовые и многомодовые. В свою очередь по профилю показателя преломления многомодовые волокна разделяются на ступенчатые (рис.5.6,а) и градиентные (рис.5.6,б). Используя принцип геометрической оптики рассмотрим вначале ступенчатые многомодовые волокна (рис.5.6а).

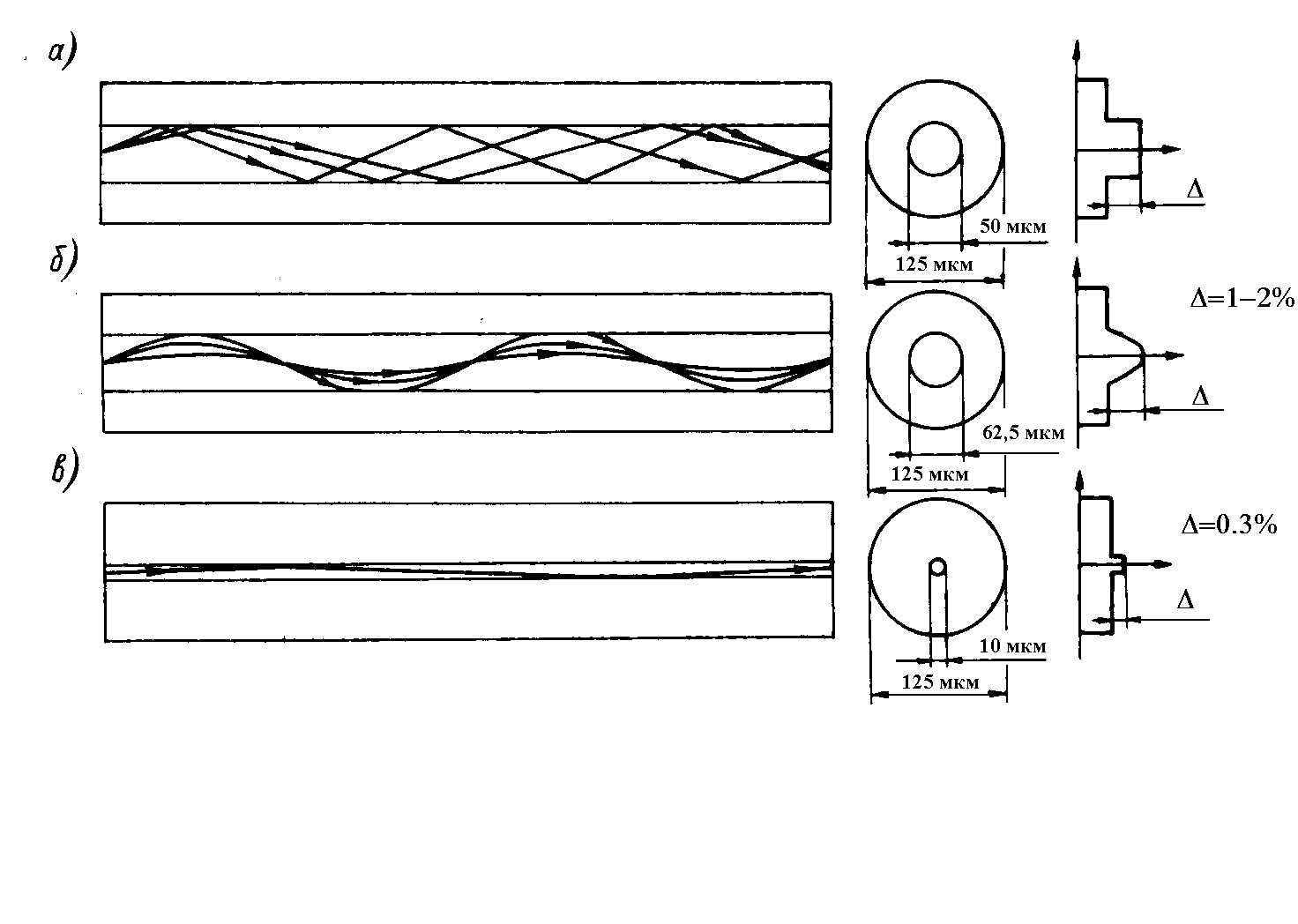
Рис. 5.6 Многомодовые и одномодовое волокна

Ступенчатым называется оптическое волокно, профиль показателя преломления в котором при переходе от сердцевины к оболочке изменяется ступенчато (скачком).

Из теории ОВ известно, что при условии V  2.405, оптическое волокно является многомодовым. При больших значениях нормированной частоты в ОВ будет существовать большое количество мод. Количество мод N при конкретном значении V (при условии, что V >>2.405) определяется как

. (5.12)

Для описания многомодовых волокон с большим количеством мод целесообразно использовать приближение геометрической оптики. В ступенчатом волокне моды высшего порядка будут соответствовать лучам, которые распространяются по ломаной траектории под самыми большими углами, т.е. самыми близкими к критическому углу; моды низших порядков соответствуют тем лучам, которые падают на поверхность раздела под малыми углами (рис. 5.6,а).

Электромагнитное поле в ОВ должно соответствовать граничным условиям на границе сердцевина–оболочка. В отличие от металлических волноводов электромагнитное поле существует и в оболочке ОВ. Поэтому часть оптической мощности распространяется и в оболочке. При уменьшении V (уменьшении числа мод) все большая часть энергии распространяется в оболочке. Это при определенных условиях, например изгибах волокна, ведет к дополнительным потерям из-за преобразования энергии направляемых мод в оболочечные моды.

Рассмотрим важный параметр многомодового волокна называемый числовая апертура. Предположим, что на торец волокна под некоторым углом _в (рис.5.7) падает оптическое излучение (показано конусом лучей). Причем внутри волокна это оптическое излучение попадает на границу сердцевина – оболочка под критическим углом _кр.

Преобразовав (5.1), можно получить следующее соотношение для синуса критического угла

.

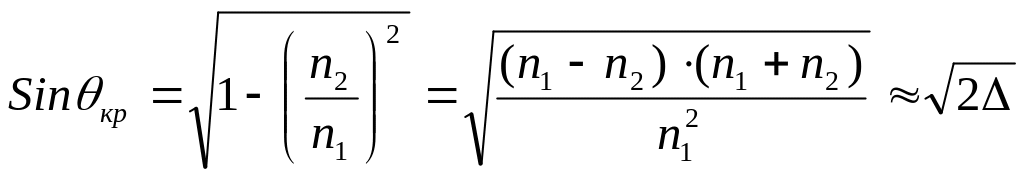Здесь принято допущение, что n₁ + n₂  2n₁.

Внешнее излучение попадает в ОВ через его торец и на границе раздела претерпевает преломление. Поэтому синус критического угла в воздухе будет в n₁ раз больше, чем в сердцевине. Обозначив произведение n₁ Sin _кр как NA, запишем

NA = Sin _внеш = n₁ Sin _кр = = . (5.13)

Это выражение и определяет параметр, называемый числовой апертурой - Numerical Aperture (NA).

Рис.5.7 Числовая апертура оптического волокна.

Числовая апертура является важным параметром волокна. В частности, NA входит в соотношения, определяющие эффективность связи оптического источника с волокном, а также потери в разъемных и неразъемных соединениях.

Различают два вида числовой апертуры – расчетную и эффективную. Расчетная числовая апертура определяется соотношением (5.13). Эффективная числовая апертура - значение, равное синусу половины плоского угла, соответствующего телесному углу, ограничивающему конус, в котором сосредоточена заданная часть мощности излучения на выходе ОВ. На выходе ОВ диаграмма излучения не имеет резкого спада, интенсивность излучения с увеличением угла постепенно уменьшается, поэтому эффективная числовая апертура не равна расчетной, а определяет тот угол, в котором сосредоточено 90% выходной мощности. Типичные значения числовой апертуры – 0.20.29.

4. Причины потерь и спектральная характеристика ов.

• поглощение в материале ОВ

• поглощение из-за примесей;

• эффекты рассеяния;

• неоднородность раздела сердцевина-оболочка при изготовлении

• излучение на изгибах.

На рис. 5.13 сплошной линией изображена спектральная зависимость поглощения для современного кварцевого ОВ. Указаны три окна прозрачности кварцевого волокна: первое - вблизи 0,85 мкм; второе – вблизи 1,31 мкм, третье –вблизи 1,55 мкм.

Как уже говорилось, увеличение потерь наблюдается при отклонении геометрии волокна от идеальной цилиндрической. К ним относятся:

- микроизгибы, т.е. отклонения оси волокна от прямолинейной с амплитудой порядка длины волны, возникающие при нанесении защитной оболочки;

- вариации поперечных сечений и элиптичность, возникающие при вытяжке;

- изгибы и скручивания, возникающие в процессе изготовления кабеля и его эксплуатации;

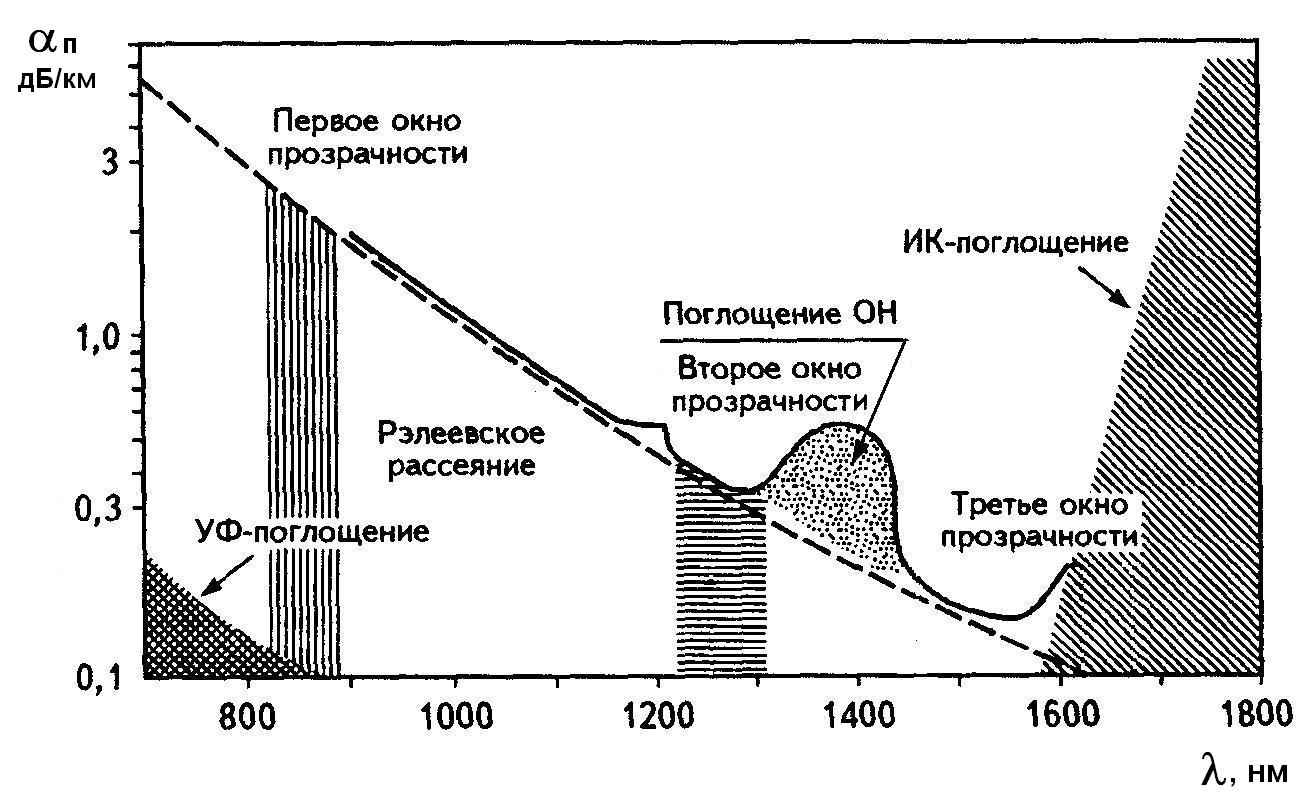
Рис.5.13 Спектральная характеристика ОВ

-неоднородности границы раздела “сердцевина-оболочка”, возникающие в процессе изготовления заготовки и вытяжки волокна.

5. Потенциальная пропускная способность.

Длина волны и частота оптического излучения связаны между собой соотношением  = с/, где с - скорость света (310⁸ м/с). Дифференцируя по , получаем d/d = -c/² . Следовательно, диапазону длин волн  соответствует диапазон частот , который определяется как

 = c/₀ ² .

Определим этот параметр для двух основных рабочих длин волн - ₀ = 1300 нм и ₀ = 1550 нм, на которых работают ВОСП. На 1300 нм при  = 40 нм  составляет  7 ТГц (710¹² Гц), на 1550 нм при  = 40 нм  составляет  5 ТГц.

Виды дисперсий:

• материальная дисперсия обусловлена зависимостью скорости оптического излучения(или показателя преломления оптического волокна n) от длины волны. В коротковолновом диапозоне(λ=0.85 мкм) в одномодовом ОВ этот тип дисперсии является преобладающим.

-величина материальной дисперсии.

Среднее время прохода оптического импулься τ по волокну длиной определяется как , -групповая скоростьимпульса в волокне. V_г = 1(dd).

удельная материальная дисперсия, это дисперсия в ОВ длиной 1 км при ширине спектра оптического источника  = 1 нм. Величина удельной материальной дисперсии в кварцевом волокне (n = 1.48) на  = 0.85 мкм составляет - –86.3 пС(нмкм) , на  = 1.55 мкм - + 15.5 пС (нмкм).

• Волноводная дисперсия – зависимость постоянной распространения оптического излучения ( а значит и его скорости) от отношения а. В В области низких значений материальной дисперсии (  1.27 мкм) преобладающей становится волноводная дисперсия. В одномодовых коротковолнового диапазона и многомодовых волокнах обычно пренебрегают этим видом дисперсии.