24. Энтропия. Закон возрастания энтропии. Третье начало термодинамики.

Энтропия - в естественных науках мера беспорядка системы, состоящей из многих элементов. Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

где — приращение энтропии; — минимальная теплота, подведенная к системе; T — абсолютная температура процесса;

Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц. Энтропия — функция состояния системы, равная в равновесном процессе количеству теплоты, сообщённой системе или отведённой от системы, отнесённому к термодинамической температуре системы.

  Закон возрастания энтропии

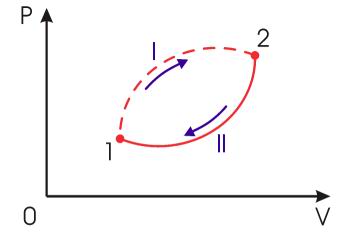
Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 3.13.

Рис. 3.13. Необратимый круговой термодинамический процесс

Пусть процесс   будет необратимым, а процесс   - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид

.

(3.55)

     Так как процесс   является обратимым, для него можно воспользоваться соотношением (3.53), которое дает

.

(3.56)

     Подстановка этой формулы в неравенство (3.55) позволяет получить выражение

.

(3.57)

     Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство

,

(3.58)

     в котором знак равенства имеет место в случае, если процесс   является обратимым, а знак больше, если процесс   - необратимый.

     Неравенство (3.58) может быть также записано и в дифференциальной форме

.

(3.59)

     Если рассмотреть адиабатически изолированную термодинамическую систему, для которой  , то выражение (3.59) примет вид

(3.60)

     или в интегральной форме

.

(3.61)

     Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом:

     В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.

     Записанное утверждение является ещё одной формулировкой второго начала термодинамики.

     Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.

     Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит локальное ее уменьшение.

     С законом возрастания энтропии непосредственно связан парадокс, сформулированный в 1852 году Томсоном (лордом Кельвином) и названый им гипотезой тепловой смерти Вселенной. Подробный анализ этой гипотезы был выполнен Клаузиусом, который считал правомерным распространение на всю Вселенную закона возрастания энтропии. Действительно, если рассмотреть Вселенную как адиабатически изолированную термодинамическую систему, то, учитывая ее бесконечный возраст, на основании закона возрастания энтропии можно сделать вывод о достижении ею максимума энтропии, то есть состояния термодинамического равновесия. Но в реально окружающей нас Вселенной этого не наблюдается.

     Попытка избежать указанного противоречия гипотезы тепловой смерти Вселенной была предпринята Больцманом, который показал, что и в состоянии термодинамического равновесия наблюдаются флуктуации термодинамических параметров. Если считать, что наблюдаемая Вселенная является следствием такой флуктуации, то противоречия парадокса тепловой смерти Вселенной снимаются. Более подробно равновесные флуктуации описаны в пятой главе.

Тепловая смерть Вселенной - это теория, выдвинутая Р. Клаузиусом в 1865, согласно которой Вселенная рассматривается как замкнутая система, поэтому согласно второму началу термодинамики, энтропия Вселенной стремится к максимуму, в результате чего со временем в ней должны прекратиться все макроскопические процессы.

Вспомним для начала, в чем заключается суть второго начала термодинамики: при протекании необратимых процессов в замкнутой системе энтропия системы возрастает. Для сравнения: в незамкнутых системах энтропия может как возрастать, так и убывать, а также оставаться без изменения.

Вернемся к нашей Вселенной. Вселенная, по мнению, Клаузиуса, является, бесспорно, замкнутой системой, так как она не обменивается энергией с другими системами (ведь не существует никакой другой Вселенной вне нашей?) Как замкнутая система, Вселенная стремится к равновесному состоянию - состоянию с максимумом энтропии. Таким образом, все происходящие во Вселенной процессы должны рано или поздно затухнуть, прекратиться.

Критика теории тепловой смерти Вселенной основывается в основном на утверждении, что, несмотря на логичность аргументов, тепловая смерть все еще не наступила. Тем не менее, мнения ученых разделились относительно будущего нашей Вселенной.

Одни ученые утверждают, что тепловая смерть Вселенной невозможна, так как второй закон термодинамики неверен или просто неточен, так как не применим ко всей Вселенной в целом. Дело в том, что состояние с максимумом энтропии можно воспринимать лишь как идеал, так как закон возрастания энтропии не носит абсолютный характер (а подчинен вероятностным законам). Другими словами, из-за случайных флуктуаций (колебаний) энтропия в системе будет всегда ниже максимума.

Еще одним аргументов против теории Клаузиуса становится понимание Вселенной как бесконечной, поэтому ее нельзя назвать ни замкнутой, ни незамкнутой системой (так как эти критерии используются для конечных объектов). Поэтому вполне логично предположить, что в условиях бесконечности второй закон термодинамики не применим в принципе, или должен быть дополнен.

В любом случае знания о Вселенной еще ничтожно малы, поэтому любые прогнозы относительно будущего Вселенной остаются лишь догадками. Например, сегодня среди ученых есть и сторонники теории тепловой смерти Вселенной, которые утверждают, что подобный сценарий развития событий должен рассматриваться наравне с другими, так как человечество до сих пор не может утверждать наверняка, является ли Вселенная бесконечной, или же она все-таки конечна, поэтому может пониматься как замкнутая система.

Третье начало термодинамики.

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю.

Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

или

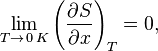
Третье начало термодинамики относится только к равновесным состояниям.

Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной , что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий в различных состояниях. Согласно третьему началу термодинамики, при значение .

В 1911 году Макс Планк сформулировал третье начало термодинамики как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: . Отсюда =0, что даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S=k ln W. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии.

Недостижимость абсолютного нуля температур

Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достичь ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры.