Физические приложения поверхностных интегралов.

1)Масса поверхности:

2)Момент инерции: – момент инерции относительно оси Ox.

3)Статический момент: – относит. плоскости YoZ

4)Центр тяжести:

Формула Остроградского-Гаусса.

Формула связ. тройной интеграл по трёхмерной обл-ти с поверхностным интегралом по поверхности, огранич. данную область.

Пусть VR³. V разбивается на конечное число элем. областей в направлении любой оси. На области заданы функции P(x,y,z), Q(x,y,z), R(x,y,z) – непр. и их частные производные также непр.   – пов-ть, кот. огранич. данную область.

Док-во. Пусть V – элементарная область в напр. оси Oz.

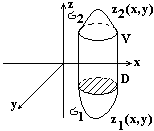
Если область разбивается на конечное число элементарных областей в направлении оси Oz, то в силу аддитивности тройного и поверхностного интеграла получ. соотношение также верно.

Аналогично получаем:

Складывая получ. соотношения получим формулу Остроградского-Гаусса.

Формула Стокса.

Связывает поверх. интеграл II-го рода с криволин. интегралом II-го рода по границе этой поверхности.

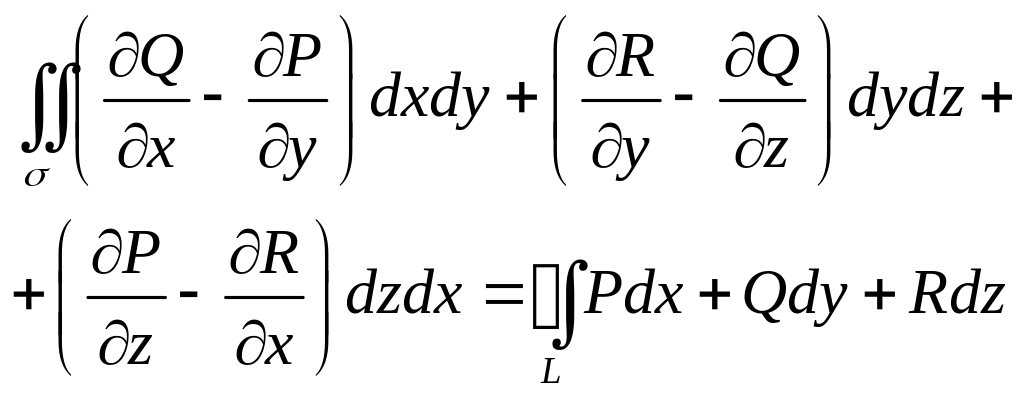P,Q,R – непрерывны, производные также непрерывны.

Док-во. 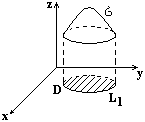Пусть поверхность задана функцией z = z(x,y), тогда 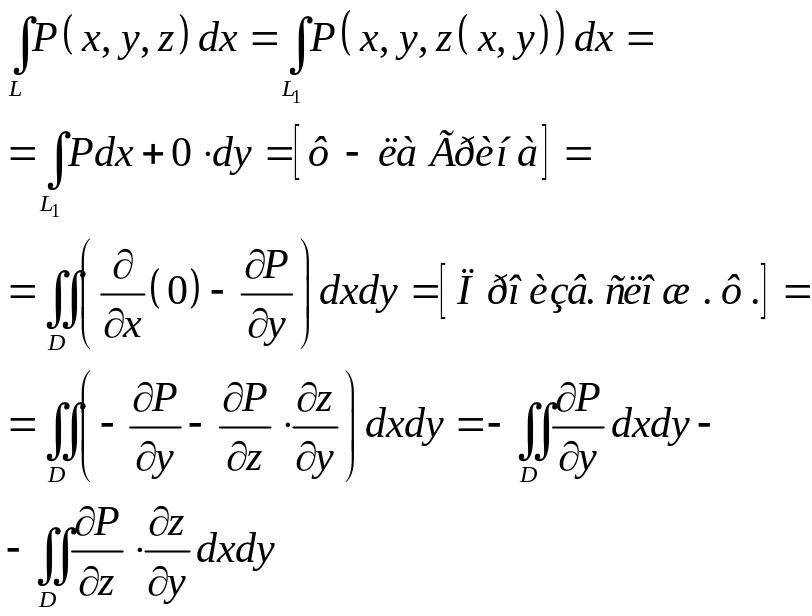Найдём производную из условия параллельности нормального вектора единичному вектору нормали {cos(),cos(),cos()}  все их координаты пропорциональны:

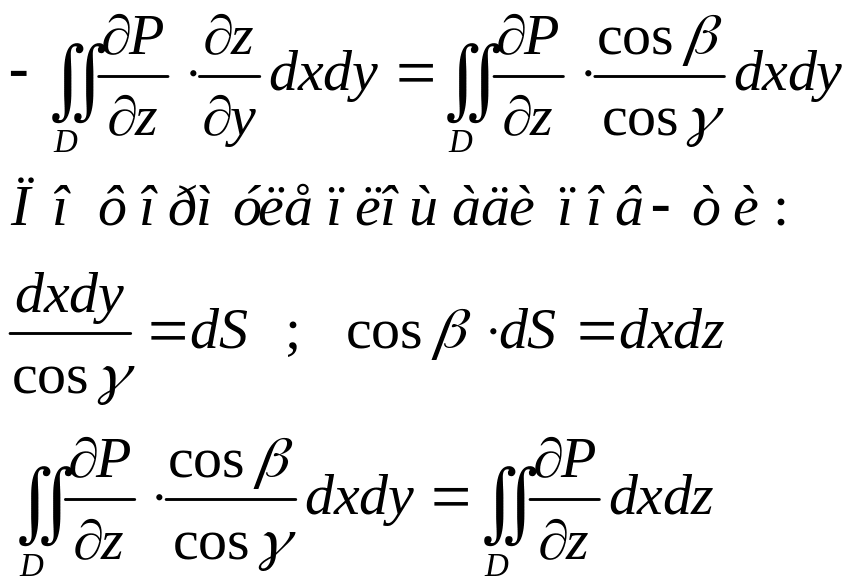
Итак получили:

Совершенно аналогично получаем:

Складывая полученные соотношения получаем формулу Стокса.

Определение и примеры несобственных интегралов I-го и II-го рода.

Несобственный интеграл – обобщение понятия определённого интеграла Римана на отрезке. Интеграл Римана определяется от ограниченной функции на ограниченном промежутке. Несобственный интеграл определяется на неограниченном промежутке.

Несобств. интеграл I-го рода. Пусть f(x) определена на [0,+∞]. Рассмотрим  A[0,+∞] и для f(x) интегрируема по Риману на [a,A].

– несобственный интеграл 1-го рода. Если этот предел существует и конечен, то интеграл сходится, а если бесконечен или не существует, то интеграл расходится.

Пример. 1)

 интеграл расходится.

2) – сходится при p>1 и расходится при p≤1.

Несобственный интеграл 2-го рода. Несобственным интегралом 2-го рода назыв. интеграл от неограниченной функции.

Пусть f(x,y) определена на [a,b), где aR, bR. b’(a,b)→f(x)R. Пусть b – особая точка: – односторонний предел.

– несобств. интеграл 2-го рода. Если предел  и он конечен, то интеграл сходится, если не  или бесконечен, то интеграл расходится.

Пример. 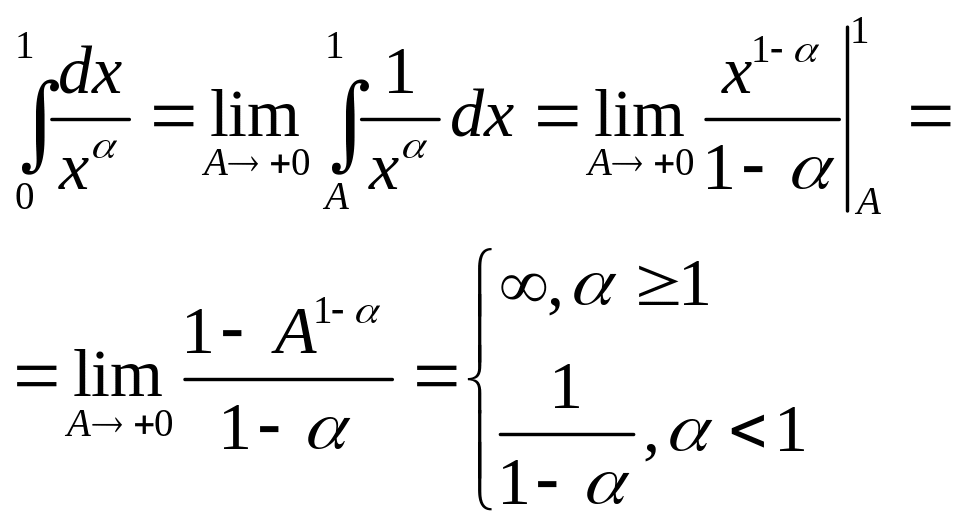Сходится при <1, расходится при ≥1.

Замечание. Для несобственного интеграла можно использовать замену переменных и интегрирование по частям. При замене переменных несобственный интеграл переходит в определённый интеграл Римана и наоборот.

Пример.

1)

2)

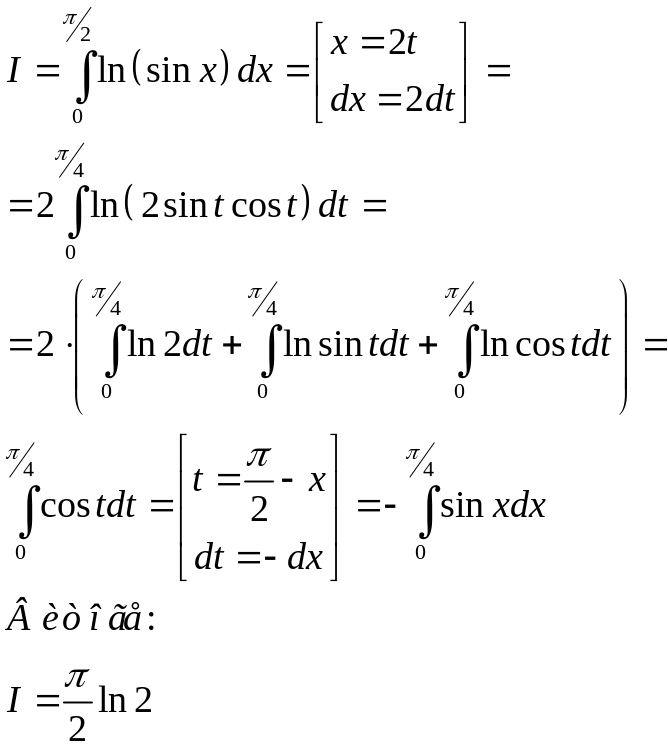
Критерии сходимости несобственных интегралов.

Объединим несобственные интегралы 1-го и 2-го рода: : 1)b=∞, 2) , bR. Пусть f(x) определена на [a,b). f(x) интегрируема на [a,b’) для b’[a,b). Пусть b’ – произвольная точка из (a,b), тогда – остаток для , где b – особая точка.

1-й критерий сходимости. 1)Если несобственный интеграл сходится, то сходится любой из его остатков, 2)Если хотя бы один из остатков сходится, то сходится и весь интеграл.

Док-во. 1)Нужно показать, что  и он конечен. По условию  предел: , тогда:

2)

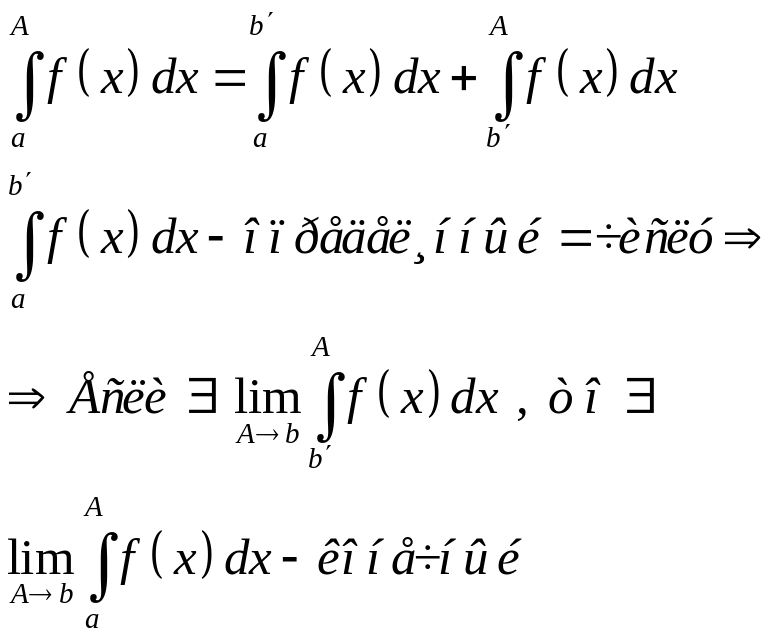
2-й критерий(критерий Коши)) – сходится  ε>0 >0 такое, что b₁(b-,b) b₂(b-,b) .

Док-во. Рассматриваем функцию , тогда сходимость несобственного интеграла означает существование такого предела По критерию коши о существовании конечного предела имеем: Предел – конечен, если ε>0  >0 b₁U_(b) b₂U_(b)  |F(b₂)‑F(b₁)|<ε

U_ = (b-,b).

3-й критерий сходимости)

Пусть f(x)≥0 x[a,b) тогда несобств. интеграл сходится  – ограничена на [a,b).

Док-во.

Необходимость. Пусть сходится  когда  конечный, а если у ф-ции  конечный предел в точке, то она ограничена в некоторой окрестности этой точки: >0 x(b-,b)

Рассмотрим F(x) на [a,b-]. Пусть x(a,b-).

Достаточность. По условию F(x) – ограничена. Покажем, что F(x) – возрастающая если x₁<x₂. x₁,x₂[a,b).

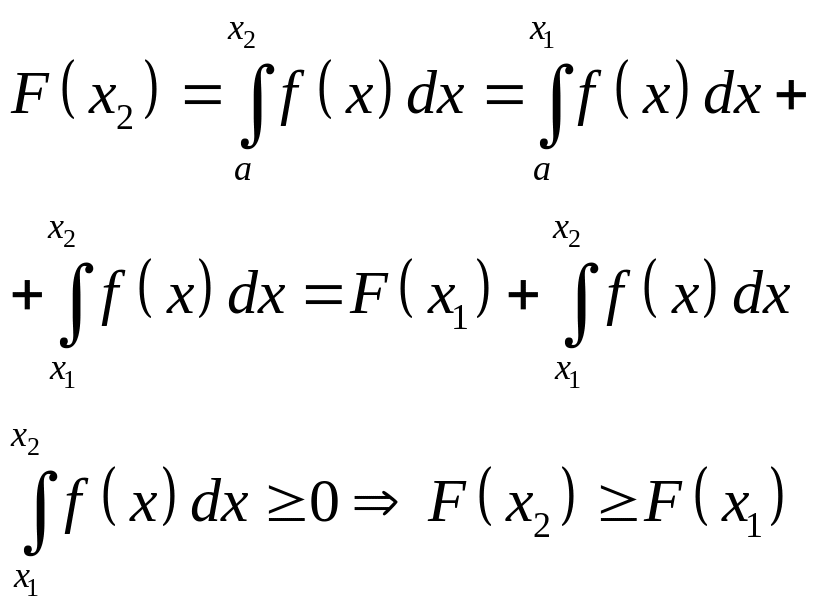
Когда функция возрастает и ограничена, то  существует конечный предел, равный супремуму.  – конечный предел  – сходится.