Тройной интеграл: определение, вычисление, св-ва, классы интегрируемых функций.

Определение. Пусть задана произвольная функция f(x,y,z) на компакте . f(x,y,z) – ограничена на компакте . Разобьём компакт  на n частей, причём так, что , а – компакт нулевого объёма. Введём понятие диаметра области: , причём . Введём понятие мелкости разбиения: . Введём понятие интегральной суммы: , где (x_i,y_i,z_i) – произвольная точка из _i. Если существует предел интегральных сумм при →0 и он не зависит не от разбиения, не от точек x_i, y_i, z_i, то такой предел назыв. тройным интегралом по области  от функции f(x,y,z). Вычисление тройного интеграла. По элементарной области. Пусть R³.  – элементарная область в направлении оси z, если область ограничена по бокам цилиндрической поверхностью || оси Oz, снизу функцией z=f₁(x,y), сверху функцией z=f₂(x,y). Пусть D – проекция области  на плоскость xOy, DR². Пусть также: 1)f(x,y,z) интегрируема в области  как функция трёх переменных, 2)для фиксированных (x,y)D функция f(x,y,z) как функция от z интегрируема на области [f₁(x,y), f₂(x,y)].

Тогда

Свойства тройного интеграла.

1)

2)

3) , – компакт нулевого объёма, тогда:

4)

5)

6)Если , то

7)Если , то

8)Если , то:

9)Теорема о среднем: Если , то  [m,M] такая, что

Классы интегрируемых функций.

Необходимое условие интегрируемости – ограниченность функции на области . Это условие не явл. достаточным. В качестве примера приведём функцию, аналогичную функции Дирихле: Верхние суммы Дарбу не совпадают с нижними.

Достаточное условие интегрируемости – непрерывность функции на .

Вычисление объёмов тел.

Док-во: Пусть f(x,y,z)=1. , – имеет нулевой объём, тогда: 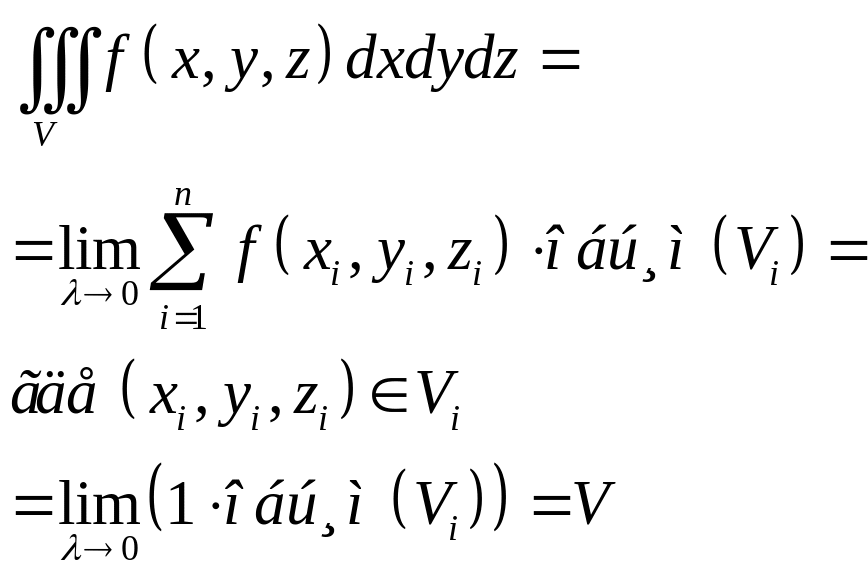Частные случаи.

1)Пусть область V – элементарная в напр. оси Oz.

2)Пусть V – элем. область, причём снизу ограничена плоскостью XoY. z₁=0, z₂=f(x,y)≥0, тогда: , где D – проекция области V на плоскость XoY.

Формула замены переменных в тройных интегралах, якобиан. Цилиндрическая и сферическая системы координат. Объём эллипсоида.

Пусть , причём  все частные производные – все непрерывные на области V.

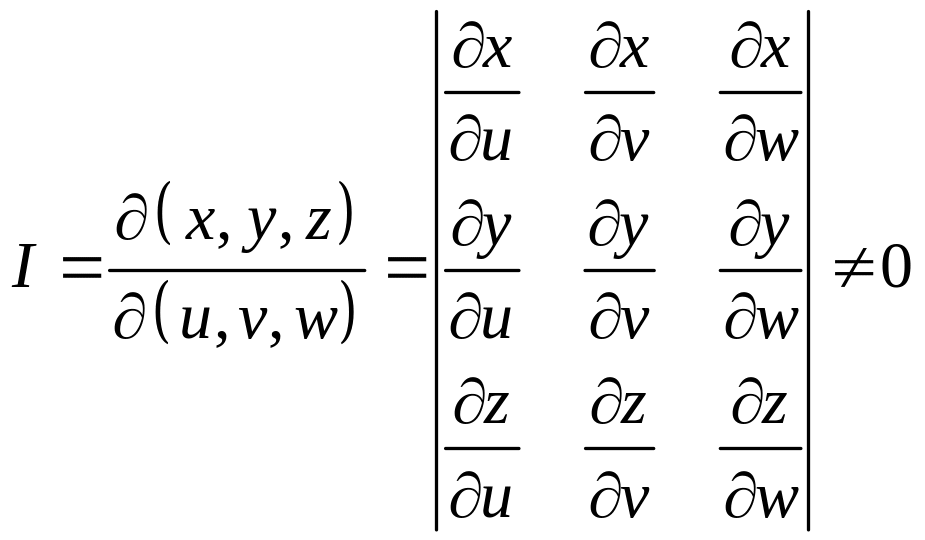
Цилиндрическая СК. – ф-ла перехода.

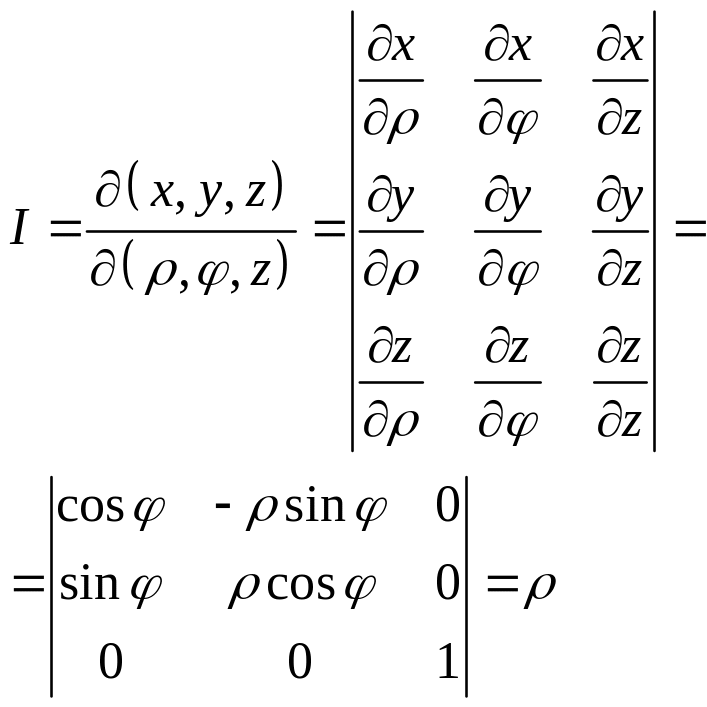
Сферические координаты.

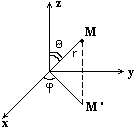
– ф-ла перехода – сферические координаты. Тогда:

Объём эллипсоида. 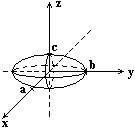Введём эллипсоидальные координаты:

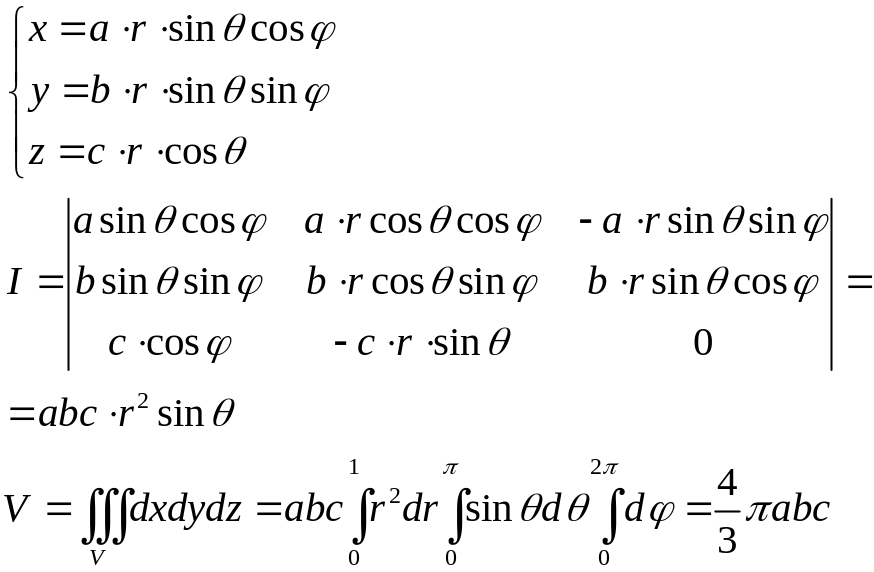
Физические приложения криволинейных интегралов: длина и масса кривой, статические моменты, момент инерции, центр тяжести кривой, работа переменной силы.

1) Длина кривой:

2)Масса кривой: , где (x,y) – ф-я плотности.

3)Статические моменты:

4)Моменты инерции:

5)Центр тяжести:

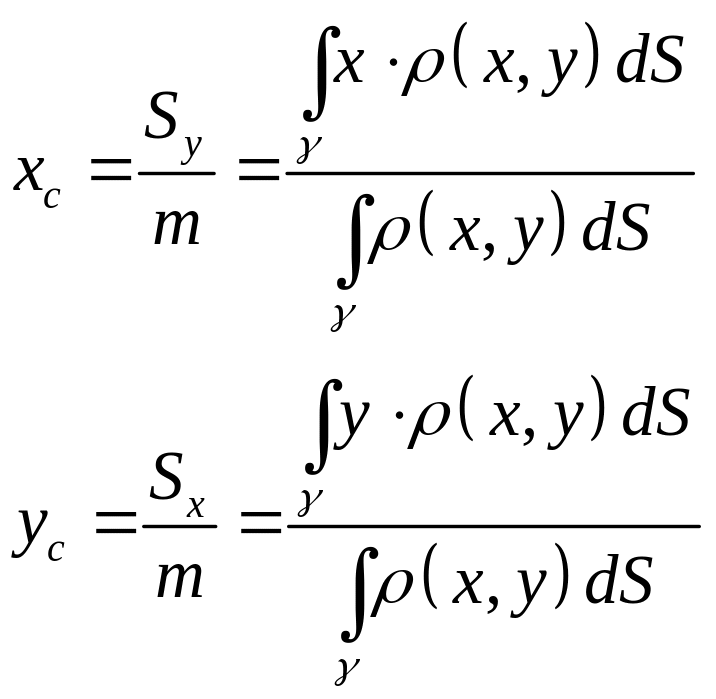
6)Работа переменной силы. Пусть некоторая сила , перемещает материальную мачку вдоль кривой , тогда работа этой силы вычисл. след. образом:

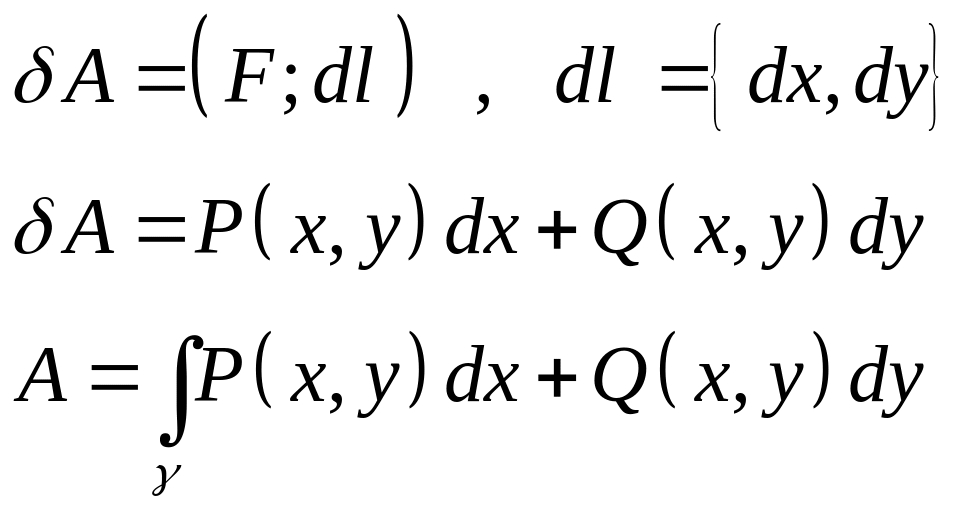
Потенциальные поля. Независимость криволинейного интеграла от пути интегрирования.

В механике очень важную роль играют особые поля, в кот. работа силы поля по перемещению матер. точки вдоль кривой зависит от начальной точки кривой и конечной точки, но не зависит от пули по кот. она проходит. Такие поля назыв. потенциальными, т.к  такая функция U(x,y) что дифференциальная форма стоящая под значком интеграла является полным дифференциалом от этой функции.  U(x,y). dU=Pdx+Qdy. , где A – начало, B – конец.

Теорема. Необходимые и достаточные условия полного дифференциала. Пусть  P(x,y), Q(x,y), – непрерывны в области D (односвязная область – т.е нет разрывов). Тогда  U(x,y) такая, что dU=Pdx+Qdy 

Док-во. Необходимость. Пусть  U(x,y) такая, что dU=Pdx+Qdy. Запиш. общ. вид полного дифф-ла: , тогда: . Найдём производные . По теореме о равенстве смешных производных они равны, т.к по условию – непрерывны.

Достаточность. Пусть . Покажем, что  U(x,y) такая, что dU=Pdx+Qdy. Из общего вида дифференциала   U можно найти из системы дифф. уравнений:

1)Интегрируем 1-е уравнение:

2)Второе уравнение запиш. в виде:

3)Из второго уравнения:

Покажем, что функция, стоящая справа не зависит от x:  правая часть уравнения не зависит от x. Независимость криволин. инт. от пути интегрирования. Если , то интеграл не зависит от пути интегрирования  можно брать любой путь (чаще всего берут путь || коорд. осям).

В случае пространственной кривой такие интегралы не зависят от пути, если дифференциальная форма является полным дифференциалом: dU=Pdx+Qdy+Rdz. . Условия  полного дифференциала: