22. Расчет цепей на синусоидальном токе.

Переменными называются токи и напряжения, изменяющиеся во времени.

Токи и напряжения, значения которых повторяются через определенное время, называются периодическими:

,

где Т – минимальный промежуток времени, через которое это равенство выполняется – период. Величина частотой. Величина называется циклической частотой.

Преимущество синусоидальных токов:

1. при трансформации форма токов и напряжений не меняется;

2. реакцией цепи на синусоидальное воздействие является синусоидальная функция той же частоты (доказательство этого утверждения оставим на первый семестр);

3. н ет помех радиоприему.

Частными случаями периодических переменных функций являются синусоидальные функции:

,

.

Рассмотрим некоторые параметры синусоидальных функций. Очевидно, синусоидальная функция характеризуется максимальным значением , частотой и сдвигом фаз . Есть еще одна характеристика синусоидальной функции – ее действующее значение:

Теперь поясним выше сказанное, отдельно взяв интеграл под корнем:

.

ВНИМАНИЕ: Амперметр всегда показывает действующее значение.

Введем понятие среднего значения – средневыпрямленное за период значение функции.

.

Рассмотрим коэффициенты, характеризующие синусоиду:

• коэффициент амплитуды:

.

• коэффициент формы:

.

Поскольку частоты воздействия и реакции цепи одинаковы, при решении задач нас будут интересовать амплитудные значения и сдвиги фаз.

23. Изображение синусоидальных величин векторами и комплексными числами.

Итак, наша задача – найти амплитудные значения и начальные фазы всех токов и напряжений. Воспользовавшись непосредственно законами Кирхгофа, получим систему интегро-дифференциальных уравнений, которая решается достаточно сложно. До проведения каких-либо расчетов посмотрим, почему возникает задача представления векторов в виде комплексных чисел.

Р ассмотрим следующую задачу (см. рисунок). Даны два тока:

Наша задача – найти . Решение:

,

тогда .

Р ешение достаточно простой задачи, где мы не имели дело с индуктивностями и емкостями, выглядит весьма громоздко. Поищем другой способ решения данной задачи. Заметим, что наш ток мы можем изобразить в виде вращающегося на плоскости против часовой стрелки вектора, обладающего длиной 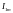, частотой вращения и начальный угол отклонения от горизонтальной оси . Тогда проекция этого вектора на вертикальную ось как раз будет изменяться по закону (см. рисунок): .

Тогда мы можем легко применить первый закон Кирхгофа к двум токам из нашей задачи: задача сложения токов сводится к сложению двух векторов (см. рисунок ниже). Такой подход к решению задачи допустим, потому что все три вектора (и исходные, и результирующий) будут вращаться на плоскости с одной и той же угловой частотой, взаимное расположение векторов в любой момент времени остается постоянным.

Совокупность векторов, отображающих синусоидальные токи и напряжения, построенных с учетом относительной ориентации и масштабов, называется векторной диаграммой.

Проводим аналогию с обобщенным комплексным воздействием. Рассмотрим комплексное число: ,

тогда модуль этого числа: ,

тогда мы можем записать: ,

г де . Возьмем нашу синусоидальную функцию и поставим ей в соответствие комплексное число: .

Мы знаем, что ,

т.е. эта величина определяет начальный сдвиг фаз на комплексной плоскости. Рассмотрим фактор : .

Это единичный вектор, который определяет направление вращения вектора тока на комплексной плоскости против часовой стрелки с угловой скоростью . Можно записать еще и следующим образом:

, где - комплексная амплитуда.

Величины, зависящие от времени: токи, напряжения, значения источников ЭДС и тока изображаются на комплексной плоскости векторами и обозначаются ( с точкой). Величины не зависящие от времени (сопротивление,..), отображаются отрезками.

Если при решении задачи с помощью комплексных числе мы нашли комплексную амплитуду, то для нахождения временной функции мы обязаны помножить эту амплитуду на и взять от полученной величины мнимую часть: .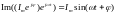

1. соответствие временных функций и комплексных величин (векторов), которое справедливо только для линейных цепей (принцип суперпозиции);

2. из двух составляющих - sin и cos - физическая реализация возможна только для синуса.

3. переход в область действительных времен (оригиналов) осуществляется путем выделения мнимой части.

24. Основная идея состояла в том, чтобы уйти от системы интегральных и дифференциальных уравнений. Путь у нас есть ток, у него есть отображение:

,

посмотрим, что происходит с его производной:

.

Мы говорили, что переход осуществляется по синусу, поэтому

.

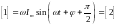Теперь переходим в область комплексных времен (изображений):

.

Вывод: В области комплексных величин операция дифференцирования заменяется умножением на фактор .

Посмотрим теперь на интеграл:

.

Вывод: В области комплексных величин операция интегрирования заменяется делением на фактор .

Теперь ясно, что мы от системы интегро-дифференциальных уравнений можем уйти в область комплексных величин, решить задачу, а потом вернуться к область действительных функций путем выделения мнимой части.

Еще мы ранее говорили о системе вращающихся векторов: у них у всех одинаковая частота. В этом мы сейчас и убедились: действительно, у всех рассматриваемых векторов есть множитель – единичный вектор, обеспечивающий вращение всей системы против часовой стрелки с одной частотой. Значит мы может рассматривать только взаимное расположение наших векторов на комплексной плоскости, а о факторе нужно вспоминать только тогда, когда переходим в область действительных времен.

Расчет синусоидальных функций с использованием комплексных величин называется комплексным или символическим методом.