
- •Классификация элементов.
- •2. Неидеальные (реальные) источники тока и эдс.
- •Неидеальные (реальные) источники тока и эдс.
- •3. Элементы, рассеивающие энергию. Резисторы.
- •4. Двухполюсник индуктивного типа.
- •5. Емкость.
- •6. Взаимная индуктивность.
- •Соотношение для идеального трансформатора.
- •7 . Многополюсник.
- •8. Зависимые источники энергии.
- •И сточник тока, управляемый напряжением: , . Это соответствует матричному уравнению:
- •12. Метод контурных токов.
- •15. Матрицы параметров цепей.
- •Записывается матрица :
- •Свойства матрицы .
- •17. Матрица инциденций.
- •18. Матрица сечений .
- •21. Метод узловых потенциалов.
- •22. Расчет цепей на синусоидальном токе.
- •23. Изображение синусоидальных величин векторами и комплексными числами.
- •25. Задача.
- •1 Способ:
- •2 Способ:
- •Важно!!!
- •27. Мощности в цепях синусоидального тока.
- •Активное сопротивление;
- •Индуктивность;
- •Емкость;
- •28. Балансы мощностей.
- •30. Резонанс токов (резонанс в параллельном контуре).
- •33. Классический метод расчета переходных процессов.
- •Переходные процессы.
- •34. Включение rl цепи на постоянное напряжение.
- •35. Включение rl цепи на источник синусоидального напряжения.
- •36. Задачи с некорректными начальными условиями.
- •37. Разряд конденсатора с начальным напряжением на rl-цепь.
- •1 Случай. Апериодический характер процесса.
- •38. Разряд конденсатора с начальным напряжением на rl-цепь.
- •2 Случай. Граничный характер процесса.
- •39. Разряд конденсатора с начальным напряжением на rl-цепь.
- •Периодический характер процесса.
- •40. Операторный метод расчета переходных процессов.
- •41. Расчет переходных процессов операторным методом.
- •Переход от изображений к оригиналам.
- •Уравнение имеет корень ;
- •43. Общие свойства четырехполюсников.
- •48. Задача на а – параметры.
- •49. Характеристические параметры четырехполюсников.
- •50. Последовательное соединение четырехполюсников.
- •51. Параллельное соединение четырехполюсников.
- •52. Каскадное соединение четырехполюсников.
- •54, Методы расчета нелинейных элементов.
- •55. Графо-аналитические методы.
- •56. Аналитические методы.
- •57. Метод Ньютона-Рафсона.
6. Взаимная индуктивность.
Э то
уже не двухполюсник, а четырехполюсник:
2 входных и 2 выходных зажима.
то
уже не двухполюсник, а четырехполюсник:
2 входных и 2 выходных зажима.
* * - одноименные зажимы.


Коэффициент взаимной индукции:
 ,
где
,
где
 - коэффициент связи, лежащий в диапазоне
- коэффициент связи, лежащий в диапазоне
 ;
;
если
 ,
то имеем дело с несвязанными
индуктивностями;
,
то имеем дело с несвязанными
индуктивностями;если
 (полная связка), то имеем дело с идеальным
трансформатором.
(полная связка), то имеем дело с идеальным
трансформатором.
Если
входной и выходной токи втекают или
вытекают из одноименных зажимов, то
имеем дело с согласным включением. Иначе
– встречное включение (на рисунках ниже
 - входной ток,
- входной ток,
 - выходной ток). Т.е. если сначала и
входной, и выходной токи сначала проходят
зажим, а затем заходят в катушку (сначала
оба проходят катушку, а потом оба входят
в зажим), то речь идет о согласном
включении.
В противном случае (один из токов втекает
в зажим, а потом идет в катушку, а другой,
наоборот, сначала проходит катушку, а
потом – в зажим), то имеем дело со
встречным
включением.
- выходной ток). Т.е. если сначала и
входной, и выходной токи сначала проходят
зажим, а затем заходят в катушку (сначала
оба проходят катушку, а потом оба входят
в зажим), то речь идет о согласном
включении.
В противном случае (один из токов втекает
в зажим, а потом идет в катушку, а другой,
наоборот, сначала проходит катушку, а
потом – в зажим), то имеем дело со
встречным
включением.
Согласное Встречное
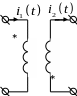


или
При согласном включении слагаемое со взаимной индуктивностью имеет тот же знак, что и слагаемое с собственной индуктивностью (а знак перед этим слагаемым зависит от условного направления тока в данной индуктивности). При встречном включении – наоборот, знаки противоположны.
Соотношение для идеального трансформатора.
Возьмем согласное включение.
 ;
;
 .
.

Как
известно, индуктивность катушки прямо
пропорциональна квадрату числа витков
 :
:
 ,
,  - коэффициент трансформации.
- коэффициент трансформации.
7 . Многополюсник.
Многополюсником называется часть цепи, имеющая более двух зажимов. (Пример: взаимная индуктивность). Рассмотрим простейший многополюсник с тремя зажимами. Как и для любого участка цепи, для него справедливы законы Кирхгофа:
 .
.
Хотя может показаться не справедливым, что три положительных числа в сумме дают ноль, но дело в том, что при записи закона мы можем выбирать произвольное направление токов на рисунке, а уже при расчетах появятся определенные знаки, которые и покажут истинное направление тока. Также справедлив и второй закон Кирхгофа:
 .
.
Т о
есть для любого трехполюсника можно
задать шесть характеристик, с помощью
которых он будет полностью описываться:
о
есть для любого трехполюсника можно
задать шесть характеристик, с помощью
которых он будет полностью описываться:
 .
Причем, зная четыре из них, мы всегда
можем найти оставшиеся. То есть 4
независимых и
2 зависимых параметра
описывают трехполюсник.
.
Причем, зная четыре из них, мы всегда
можем найти оставшиеся. То есть 4
независимых и
2 зависимых параметра
описывают трехполюсник.
Рассмотрим конкретный
пример трехполюсника, а именно транзистор.
Как известно
транзистор имеет базу,
эммитор и
коллектор.
Транзистор описывают четыре независимые
переменные:
 (других быть просто не может). Получаем
семейство из двух вольтамперных
характеристик: базовая
и коллекторная.
(других быть просто не может). Получаем
семейство из двух вольтамперных
характеристик: базовая
и коллекторная.
Осн.
ур-ния: З-ны
Киргофа : _
_
Уравнения баланса
мощности:

8. Зависимые источники энергии.
И
 сточник
ЭДС, управляемый напряжением:
сточник
ЭДС, управляемый напряжением:
Рассмотрим четырехполюсник,
изображенный на рисунке. Можем сказать,
что
 - разрыв цепи, а
- разрыв цепи, а
 .
Четырехполюсники описываются матричными
уравнениями,
поэтому, чтобы иметь возможность
моделировать зависимые источники
энергии, запишем полученные уравнения
в матричном виде:
.
Четырехполюсники описываются матричными
уравнениями,
поэтому, чтобы иметь возможность
моделировать зависимые источники
энергии, запишем полученные уравнения
в матричном виде:
 .
.
И сточник тока, управляемый напряжением: , . Это соответствует матричному уравнению:
Источник ЭДС , управляемый током:
Т ок
в первой цепи должен протекать, тогда
ок
в первой цепи должен протекать, тогда
 (кинули закоротку),
(кинули закоротку),
 .
. 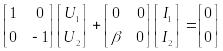
И
 сточник
тока, управляемый током:
сточник
тока, управляемый током:
Это, как раз, наш
транзисторный источник тока:
 .
Тогда:
.
Тогда:

Итак, коллекторный ток управляется током, который мы загоняем в базу транзистора. Однако не только источником тока, управляемым током, стоит какая-то физическая модель. Об этом в следующей теме.
9.
1 0.
0.

11.
