55. Графо-аналитические методы.

Э тот метод, как следует из названия, совмещает элементы графического и аналитического методов. ВАХ нелинейных элементов должна быть задана графиком. В данном методе главная проблема состоит в определении рабочей точки. Предположим, рабочую точку нам определить удалось. Как нам уже известно, .

Т огда напряжение на нелинейном элементе в окрестности рабочей точки будет описываться выражением: ,

где - напряжение на нелинейном элементе в отсутствие тока, что соответствует эквивалентной схеме, изображенной на рисунке. Разделив полученное выражение на , получим ток через нелинейный элемент: .

Вводя обозначение , получим, что , что соответствует эквивалентной схеме с источником тока.

О днако ВАХ нелинейного элемента может иметь вид, сходный, например, с характеристикой диода, т.е. для данной характеристики касательная в рабочей точке пересекает ось напряжений в точке . В этом случае эквивалентные схемы строятся точно так же с точностью до направления полярности источника и : .

Для схемы с источником тока:

.

Эквивалентные схемы для обоих случаев изображены на рисунках ниже.

И так, определим порядок расчета нелинейных элементов графо-аналитическим методом:

• определяем рабочую точку;

• строим линеаризованную схему замещения нелинейного элемента;

• проводим расчет для линейного участка любым известным методом.

56. Аналитические методы.

Р ассмотрим следующую задачу: активный двухполюсник нагружен на нелинейный элемент, нужно определить ток и напряжение через нелинейный элемент. При помощи метода эквивалентного генератора строим эквивалентную схему замещения. Очевидно, при аналитических методах расчета ВАХ нелинейного элемента должна быть задана аналитически. Пусть в нашей задаче

.

Определим для нашей задачи и параметры эквивалентного генератора (см. рис.). Запишем 1-й закон Кирхгофа:

.

В аналитических функциях в общем виде решить данное уравнение невозможно. Решение находят с помощью итерационных методов или итерационных процедур. Итерационные методы предполагают:

1. задание алгоритма;

2. задание начальной точки.

Воспользуемся методом деления отрезка пополам. Ввиду того, что мы рассматриваем электрическую цепь, функция будет монотонна. А это значит, что если мы возьмем точку примерно в середине интервала, на котором мы рассматриваем исходную функцию, то знак полученного значения совпадет со знаком на одном из концов интервала. Затем подобными манипуляциями рассчитываем ноль функции до тех пор, пока не будет достигнута требуемая степень точности. График функции изображен на рисунке. Запишем алгоритм решения задачи:

1. на правом конце интервала ;

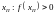2. на левом конце интервала ;

3. находим среднее значение на интервале: ;

4. дальнейшие действия определяются знаком : если знак совпадает со знаком , тогда заменяем на и проводим расчет снова. Аналогично для случая, если знак совпадает со знаком .

Отметим, каким образом нужно выбирать пределы интервала.

1 граница: напряжение на линейном элементе отсутствует, .

2 граница: предельное значение напряжения на нелинейном элементе (в данном случае, когда напряжение на нелинейном элементе равно напряжению источника ЭДС).

В условиях данной задачи:

Недостатки алгоритма:

• линейная сходимость;

• применимость только для цепей с одним нелинейным элементом.