43. Общие свойства четырехполюсников.

Ч етырехполюсники – это устройства, служащие для передачи энергии или сигнала и имеющие 2 входных и 2 выходных зажима.

П римеры четырехполюсников:

• взаимная индуктивность (трансформатор);

• фильтр;

• транзистор (трехполюсник, но может

рассматриватся как четырехполюсник);

• аналогично, операционный усилитель.

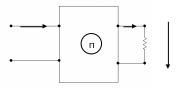
Четырехполюсники бывают активные и пассивные. Пассивные не содержат в своем составе источников энергии, или они взаимно скомпенсированы. Активные четырехполюсники содержат в своем составе нескомпенсированные источники энергии. Будем рассматривать свойства четырехполюсников на синусоидальном токе.

Итак, есть входные и выходные токи и напряжения. Направление токов и напряжений выбираем таким образом, чтобы оно соответствовало передаче энергии от источника (первичных зажимов) в нагрузку. Описать четырехполюсник – значит найти связь между парами входных и выходных токов и напряжений.

Запишем по МКТ уравнения для нашей цепи ( собственные сопротивления контуров четырехполюсника):

Обозначим - наше выходное напряжение, тогда:

По правилу Крамера решаем систему: .

Понятно, что - проводимость. Введем следующие обозначения:

, , , ,

тогда связь между входными и выходными токами и напряжениями будет выглядеть следующим образом:

Это система уравнений получила название «система в параметрах».

44.

45.

46.

47.

48. Задача на а – параметры.

Зная результаты измерений, вычислим А – параметры и затем построим эквивалентную схему замещения.

Дано:

В результате опытов были получены следующие данные:

В. В. В.

А. А. А.

кВт. кВт. Вт.

.

Решение:

Итак, определим

Определим

,

Проделав аналогичные вычисления, получим, что

.

Определяем параметры:

,

а нам взять неоткуда. Воспользуемся такой формулой:

,

тогда

.

Теперь можем определить наши параметры:

.

Теперь построим Т – образную схему замещения:

.

.

Т аким образом, эквивалентная схема замещения будет иметь вид, изображенный на рисунке.

49. Характеристические параметры четырехполюсников.

Здесь мы как раз обращаемся к той самой 6-й системе, описывающей четырехполюсники: системе в характеристических параметрах.

П ассивный четырехполюсник, изображенный справа, описывается следующей системой:

Посмотрим на : .

В озьмем тот же самый четырехполюсник, поставим на вход сопротивление и посмотрим на входное сопротивление со стороны вторичных зажимов -

с учетом того, что токи будут протекать в обратном направлении. Т.е. получили очень любопытную вещь:

Т.е. наш четырехполюсник является преобразователем сопротивления. Т.е. сопротивление нагрузки источник, подключаемый ко входным зажимам, воспринимает как совершенно другое, преобразованное сопротивление. Аналогично для нагрузки.

Р ассмотрим цепь, изображенную справа; здесь сопротивление генератора, сопротивление нагрузки. Одна из задач радиоэлектроники – передача максимальной мощности от источника в нагрузку. Т.е. задача в том, чтобы обеспечить согласованный режим работы генератора и нагрузки (их сопротивления должны отличаться только знаком мнимой части).

И так, пусть в общем случае сопротивления генератора и нагрузки несогласованны. Тогда мы включаем для их согласования пассивный четырехполюсник (см. рисунок), который как раз и обеспечит режим согласования. При согласовании генератора с нагрузкой четырехполюсник содержит только реактивные элементы (если добавить активный элемент, на нем будет только рассеиваться мощность). Наши характеристические параметры как раз и служат для обеспечения согласованного режима.

Выберем и таким образом, чтобы два уравнения выполнялись одновременно:

Решив эту систему уравнений, найдем:

Введем следующие обозначения:

Вспомним: .

Тогда:

Вспоминаем об параметрах:

В общем случае комплексная величина:

коэффициент затухания или коэффициент амплитуды, коэффициент фазы.

Согласованный режим работы означает, что

,

здесь . В согласованном режиме отношение амплитуд будет определяться так:

Коэффициент показывает затухание. Чтобы окончательно прояснить физический смысл, рассмотрим симметричный четырехполюсник, у которого .

Тогда для симметричного четырехполюсника получаем: .

Теперь ясно, почему коэффициент амплитуды. Единицы измерения коэффициента затухания: - непер. 1 Нп соответствует затуханию амплитуды в е раз. .

В радиотехнике принята еще одна единица затухания – Бэл – это отношение кажущихся мощностей:

Один Бэл соответствует затуханию амплитуды в 10 раз, два Бэла – в сто раз! Единица измерения децибел - в 10 раз меньше:

.

.

соответствует затуханию амплитуды в раз.