Периодический характер процесса.

Данный случай характеризуется выражением , т.е. корни характер-ого уравнения и - комплексно сопряженные величины. Введем следующие обозначения: , .

Тогда .

Найдем выраж для тока в конт: .

Получили периодическую зависимость тока от времени, отсюда и название случая.

.

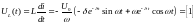Введем новые переменные и следующим образом: 1)

2) .

Разделим и умножим выражение для на :

.

Найдем оставшуюся временную зависимость на конденсаторе. Имеем:

,

тогда .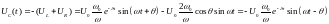

З аметим, что в данном случае мы имеем две постоянных времени.

График зависимости тока от времени будет иметь вид:

.

В общем виде график такого плана строится следующим образом. Очевидно, у этого графика есть 2 асимптоты – огибающие синусоиды, ведь график функции представляет собой синусоиду, амплитуда которой уменьшается по экспоненциальному закону.

Первая постоянная времени характеризует асимптоты-экспоненты, а вторая - - частоту синусоидальной функции.

Теперь займемся построением графиков непосредственно токов и напряжений. Выпишем для наглядности полученные временные зависимости:

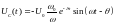
График тока (а значит и напряжения на резисторе) будет иметь такую же структуру, как только что рассмотренный, только взятый с противоположным знаком (действительно, при замыкании контура конденсатор начинает разряжаться).

Из формулы следует, что график напряжения на индуктивности начинается из отрицательной области (в начальный момент времени), а график напряжения на конденсаторе – из такого же по модулю и противоположного по знаку значения. Напряжение на индуктивности уже достигло своего максимального значения и после коммутации спадает (по модулю), а на емкости – только приближается к максимальному значению. Исходя из этих соображений, можно качественно построить графики.

Отметим, что если , то , , т.е. график будет без затуханий: действительно, мощность не будет рассеиваться на активном элементе.

40. Операторный метод расчета переходных процессов.

Смысл операторного метода расчета – переход от дифференциальных уравнений к линейным. Если функция удовлетворяет условию Дирихле: является непрерывной или имеет на конечном интервале времени конечное число разрывов первого рода и конечное число максимумов и минимумов, и 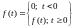, то данная функция представима в виде: , где - оператор Лапласа.

Интеграл имеет конечное значение в том случае, если растет не быстрее, чем : ,

где и - конечные вещественные числа, причем . Подобное преобразование функции получило название преобразование Лапласа.

Следующий интеграл представляет собой обратное преобразование Лапласа – переход из области изображений в область оригиналов:

Размерность переменной (т.е. тока или напряжения) в области изображений равна размерности оригинала, умноженной на секунду. Существует т.н. преобразование Карссона, для которого размерность изображения совпадает с размерностью оригинала: .

Итак, с помощью преобразования Лапласа определим изображение функции :

, где L – оператор Лапласа. Рассмотрим свойства функций и :

1. Если , то .

2. Если и , то .

3. Пусть , тогда 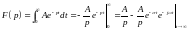, где 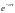- затухающая функция при , а - единичный вектор, т.е. получаем произведение затухающей функции на ограниченную, которое в пределе дает 0, поэтому .

4. Пусть , найдем изображ ф-ции :

Снова возникает неопределенность в верхней подстановке, т.е. при . Для того, чтобы интеграл имел конечное значение, должно расти не быстрее чем 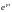(см. начало лекции). Поэтому затухает быстрее, чем растет . Поэтому произведение этих функций при стремится к нулю, а значит , таким образом, .

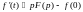В общем случае для производной n-го порядка при ненулевых начальных условиях имеем:

.

При нулевых начальных условиях имеем: .

5. Пусть , найдем изображение функции :

Нижняя подстановка в первом слагаемом, очевидно, = 0. Поскольку функция растет не быстрее, чем , интеграл тем более будет расти не быстрее, тогда и верхняя подстановка в первом слагаемом в пределе обращается в ноль, тогда , т.е. ,

причем это выражение справедливо как при нулевых, так и при ненулевых начальных условиях.

!ВАЖНО! В общем случае преобразование Лапласа для ненулевых начальных условий отличается от преобразования для нулевых начальных условий (см. свойство 4).

Рассмотрим конкретные примеры: найдем изображения по Лапласу токов и напряжений на реактивных элементах. Пусть , найдем изображение функции :

.

Теперь найдем изображение функции : .

Не забываем о том, что изображением константы по Лапласу является эта константа, умноженная на р, тогда ,

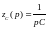эти значения получили название операторные сопротивления индуктивности и емкости соответственно.

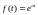6. Пусть , найдем изображение этой функции; ,

верхний предел обращается в ноль из тех же соображений, что и в предыдущих случаях.

7. Пусть , найдем изображение этой функции, сведя этот случай к предыдущему. Интеграл брать непосредственно мы не будем, а воспользуемся выражением комплексного синуса через экспоненты: .

Аналогичное выражение можно получить для : .