37. Разряд конденсатора с начальным напряжением на rl-цепь.

В цепи нет источника, но зато содержится 2 реактивных элемента: катушка и емкость, обладающая напряжением в начальный момент времени. По второму закону Кирхгофа,

Продифференцируем уравнение по времени:

Определим ток в цепи:

Поскольку в цепи нет источника, , тогда ,

где и - корни характеристического уравнения: ,

откуда .

Запишем начальные условия: .

До коммутации ток через инд-ть не протекал, , с др. стороны, .

Применим 2-й закон коммутации: .

В момент времени .

Тогда .

Решая совместно и , получим: .

Отсюда найдем ток: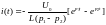

Упростим полученное выражение для . Пусть

,

отметим, что

Подставив это равенство в выражение для , получим: ,

где .

Итак, мы рассмотрели решение данной цепи в общем случае. Рассмотрим далее частные случаи и в зависимости от предполагаемых значений и попытаемся построить графики токов и напряжений. Возможны 3 случая в зависимости от того, что получится в подкоренном выражении в формуле для :

1. и отрицательны и различны, ;

2. и отрицательны и совпадают, ;

3. и представляют собой пару комплексно сопряженных чисел, .

1 Случай. Апериодический характер процесса.

В этом случае являются различными действительными отрицательными числами: , кроме того, ,

поскольку мы выбрали , тогда .

Наша задача - построить графики токов и напряжений, не зная численных значений элементов цепи. Ток в контуре начинается и заканчивается в нуле (в начальный момент времени цепь разомкнута, а после замыкания ключа в цепи нет источника, чтобы поддерживать ток). Значит, ток должен достигать максимального (по модулю) значения, причем это значение всегда будет отрицательным (см. формулу для значения тока с учетом выбранных значений и ), что с точки зрения физики процесса означает разрядку конденсатора. Построим графики тока в контуре и напряжений на емкости и индуктивности (очевидно, график напряжения на сопротивлении будет повторять график тока с неким коэффициентом ).

В начальный момент времени напряжение на индуктивности = , при (выражение для индуктивности представляет из себя суперпозицию двух экспонент). При максимальном значении тока в контуре значение напряжения на индуктивности должно = 0 (с физической точки зрения, все напряжение от конденсатора приложено к сопротивлению, а с математической, чтобы найти максимум функции, нужно приравнять к нулю производную этой функции и найти корни полученного уравнения; производная тока по времени с точностью до коэффициента равна ).

Напряжение на конденсаторе в начальный момент времени по 2-му закону коммутации , а при это напряжение падает до нуля.

Теперь рассмотрим максимумы напряжений на индуктивности и сопротивлении в моменты времени и . Как говорилось выше, максимум тока в контуре будет определяться из условия

.

Максимум напряжения на индуктивности в момент времени определяется из условия

.