1. Электрической цепью называется система заряженных частиц и проводников с током, которые могут быть описаны такими интегральными понятиями, как ток (I), напряжение (U), ЭДС , мощность и энергия , или для мгновенных значений , , , и соответственно.

Элементы цепи – то из чего состоит цепь; они призваны отображать одно из нескольких свойств:

1. генерировать энергию или преобразовывать другие виды энергии в электрическую;

2. рассеивать энергию;

3. накапливать энергию в магнитном поле;

4. накапливать энергию в электрическом поле.

Понятно, что реальные элементы каким-либо одним свойством обладать не могут (катушка индуктивности – это и провод (сопротивление), и индуктивность; а так как работаем на высоких частотах, возникает еще и межвитковая емкость. Итого – 2, 3 и 4 пункты). Мы будем использовать математические модели элементов.

Классификация элементов.

Элементы бывают:

1. линейные (с постоянными параметрами) и нелинейные (с параметрами, зависящими от токов и напряжений); соответственно различают линейные и нелинейные цепи;

2. элементы с параметрами, зависящими от времени – параметрические элементы; иначе элементы называют время-инвариантными.

3. Элементы с сосредоточенными параметрами – если ток через любое сечение элемента неразветвленной ветви в любой момент времени t остается постоянным, т.е. . Если же ток зависит от координаты, то имеем дело с элементами с распределенными параметрами.

Конечно, элементы могут комбинировать несколько свойств (линейные с сосредоточенными параметрами и т.п.).

Л юбая часть цепи, содержащая 2 зажима, называется двухполюсником. Двухполюсники бывают активные и пассивные. Пассивным принято считать двухполюсник, для которого

.

Математическое определение: активный двухполюсник содержит в своем составе нескомпенсированные источники энергии; пассивный не содержит источников энергии, либо они взаимно скомпенсированы.

2. Неидеальные (реальные) источники тока и эдс.

Основные свойства идеала:

• разность потенциалов на зажимах идеального источника ЭДС не зависит от величины и направления протекающего тока;

• величина и направление тока в ветви с идеальным источником тока не зависит от разности потенциалов на зажимах источника.

Неидеальные (реальные) источники тока и эдс.

Реализовать идеальный источник тока или ЭДС на практике невозможно. Значит, неидеальные источники тока и ЭДС будут выглядеть следующим образом:

Неидеальный источник ЭДС Неидеальный источник тока

Посмотрим, как изменятся вольт-амперные характеристики. Теперь для неидеального источника ЭДС в зависимости от протекающего тока разность потенциалов будет меняться. Очевидно, будет наблюдаться падение напряжения (ток через внутреннее сопротивление течет от + к –). Значит и характеристика будет падающей. Аналогично для неидеального источника тока, падение напряжение будет происходить на внутренней проводимости.

Заметим, что характеристики неидеальных источником тока и ЭДС практически ничем не отличаются, разве что наклоном к вертикали. Этого достаточно, чтобы преобразовать неидеальный источник ЭДС в неидеальный источник тока, и наоборот. Построим по двум известным точкам (значения тока и напряжения на координатных осях) общую прямую для неидеальных источников:

При совпадении характеристик мы получаем, что . Т.е. мы можем преобразовать неидеальный источник ЭДС в неидеальный источник тока, и наоборот. Идеальный источник тока к идеальному источнику ЭДС и наоборот преобразовать невозможно.

Это есть пример эквивалентного преобразования элементов. Преобразование считается эквивалентным, когда для внешней цепи токи, напряжения и мощности (внешние характеристики) сохраняются. С внутренними дело обстоит несколько по-другому. Рассмотрим этот случай.

В озьмем цепи, состоящие из неидеальных источников (тока и напряжения) и нагрузки.

В случае для источника ЭДС ток через нагрузку 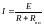, значит, мощность, которая выделяется на нагрузке, равна: .

Т еперь рассмотрим аналогичную схему с источником тока. По нашему эквивалентному преобразованию, . Тогда ток, который будет протекать через нагрузку, будет равен: .

Тогда для мощности получаем:

Т.е. при таком изменении сохранились напряжение и мощность на нагрузке.

Посмотрим, что происходит с внутренними соотношениями. Для этого вычислим мощность, выделяющуюся на внутреннем сопротивлении источников.

В первом случае (для источника ЭДС ):

Во втором случ (для источника тока ):

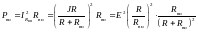
Если , то внутренние соотношения при эквивалентном преобразовании цепей в общем случае не сохраняются.