3.4.7. Діаграма енергомас, розрахунок tgmax, tgmin

Маючи графіки залежностей =f() і Е=f(), побудуємо графік залежності Е=f( ) – діаграму енергомас, для цього проводимо довільну лінію під кутом 45 з якою з’єднуємо всі лінії що виходять з точок на графіку . Потім з отриманих точок проводимо перпендикуляри, які перетинаються з паралельними прямими, що виходять з графіка . Таким чином отримавши точки від 1 до 12, які з’єднуємо послідовно.

Розрахуємо тангенси кутів tg_max, tg_min за відомим коефіцієнтом нерівномірності руху механізму =0,015:

;

Визначимо значення кутів:

_max=arctg_max=arctg 0,064=3,66;

_min=arctg_min=arctg 0,048=2,7.

Під кутами _max та _min проводимо дві дотичні до діаграми. Дотичні перетинають вісь T діаграми у точках а і b. З графіка визначаємо відстань між цими точками [0b]=18 мм.

3.4.8. Визначення параметрів маховика

За отриманими даними визначаємо момент інерції маховика для 1-го положення:

Приймемо, що маховик конструктивно виконаний у вигляді сталевого диску. Визначимо його розміри:

• діаметр

• товщина

де - густина сталі, - відношення товщини диску до його діаметру.

• маса маховика

Рисунок6.Конструкція маховика.

3.5. Висновки

При виконанні структурного та кінематичного аналізу кривошипно-шатунного механізму було визначено, що це механізм 2-го класу, 2-го порядку, знайдено кут розмаху механізму. Побудовано плани дванадцяти положень механізму, а також плани швидкостей та прискорень точок і ланок для відповідних положень даного механізму. Виконано розрахунки для цих планів та знайдені значення швидкостей та прискорень всіх ланок. У результаті динамічного аналізу було знайдено параметри маховика.

4. Кінетостатичний аналіз механізму

4.1. Задачі

В теорії машин і механізмів досить широке використання набув метод кінетостатичного силового розрахунку механізму. Він полягає в наступному. Якщо до точок невільної системи разом із заданими силами прикласти умовно фіктивні для цієї системи сили інерції, то сукупність цих сил врівноважується реакціями зв’язку. Цей прийом, незважаючи на його умовність, має таку важливу для практики перевагу, що дозволяє звести вирішення задач динаміки до вирішення задач статики.

Кінетостатичний метод розрахунку дозволяє, як вказано вище, знаходити реакції в кінематичних парах, чи, інакше кажучи, визначати ті тиски, які виникають в місцях дотику елементів кінематичних пар, а також знаходити врівноважуючи силу чи врівноважуючий момент пари сил.

4.2. Синтез інерції ланок. Сили, що діють на ланки механізму

Сили інерції ланок визначаються за формулою:

,

де m_i – це маса ланки, а - величина прискорення її центру мас.

Маса ланки визначається за формулою:

,

де - довжина ланки, а - її питома вага, яка задана за умовою.

За наведеними формулами визначаємо сили інерції ланок:

• для 1-го положення:

• для 10-го положення:

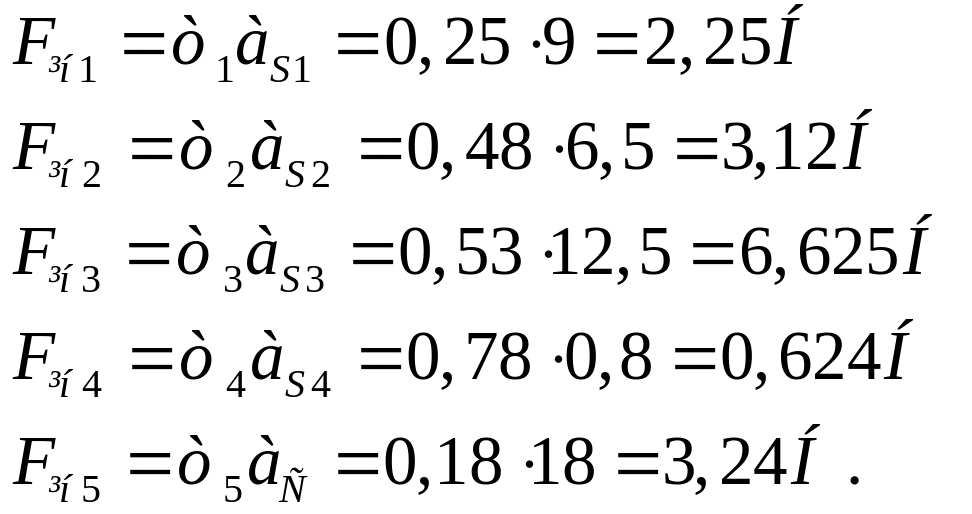
Визначаємо реакції в кінематичних парах групи Ассура (4;5). Будуємо в масштабі групу Ассура і прикладаємо до її ланок сили:

силу реакції ланки 4 на ланку 1 - прикладаємо в точці C₁. Цю реакцію розкладаємо на 2 складові – нормальну напрямлену вздовж ланки D₁C₁ і дотичну , напрямлену перпендикулярно до D₁C₁.

силу реакції ланки 0 (стояка) на ланку 5 - довільно прикладаємо в точці .

Визначаємо величину , для чого складаємо рівняння моментів відносно точки С₁:

Вимірюємо величину ланки з креслення:

• для 1-го положення:

• для 10-го положення:

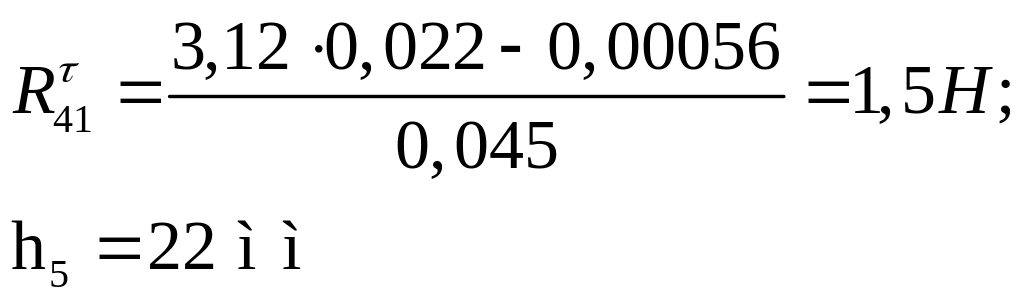
Моменти сил інерції ланок визначаємо за формулою:

• для 1-го положення:

• для 10-го положення:

Будуємо план сил для групи Ассура (4,5), для чого складаємо векторне рівняння:

Задаємося масштабом: і визначаємо величини відрізків:

• для 1-го положення:

• для 10-го положення:

Відповідно до векторного рівняння послідовно складаємо відомі вектори. Складаючи відповідні із них, отримуємо вектори та . Визначаємо їх величини:

• для 1-го положення:

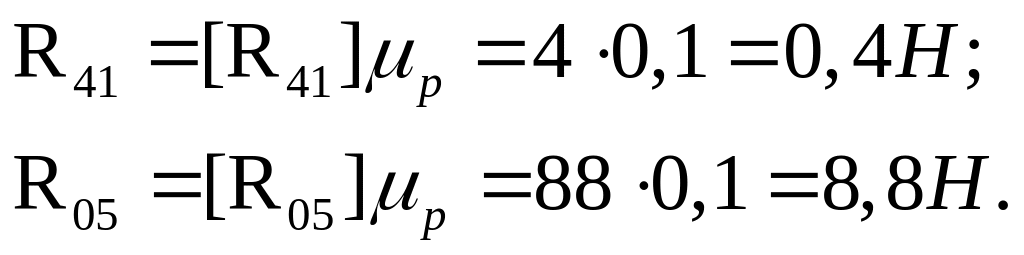
• _{для 10-го положення:}

Визначаємо реакції в кінематичних парах групи Ассура (2,3). Для цього викреслюємо в масштабі положення групи Ассура і прикладаємо до її ланок сили:

силу реакції стійки на ланку 3- прикладаємо в точці перпендикулярно напрямній х-х

силу реакції ланки 2 на ланку 4 - прикладаємо у точці і розкладаємо її на дві складові - нормальну направлену вздовж ланки і дотичну

силу реакції ланки 2 на ланку 3 - прикладаємо перпендикулярно АО;

Визначаємо величину , для чого складаємо рівняння моментів, що діють на ланку 2 відносно точки А:

Вимірюємо величини плечей з креслення:

тоді

• для 10-го положення:

тоді:

Будуємо план сил для групи Ассура (2-3) за векторним рівнянням:

Попередньо задаємося масштабом сил і вираховуємо довжини відрізків, які необхідні зобразити ці вектор на плані сил:

• для 1-го положення:

• для 10-го положення:

У відповідності до рівняння послідовно складаємо відомі вектори , , Через початок вектора проводимо напрям вектора , а через кінець вектора – напрям вектор . Складаючи вектори і (тобто з’єднуючи початок вектора із кінцем вектора ), отримаємо вектор

Вимірюємо на плані сил відрізки, які зображують відповідні вектори сил:

• для 1-го положення:

• для 10-го положення:

Розрахунок кривошипа:

Прикладаємо до кривошипа сили:

Сила інерції через точку направлена протилежно прискоренню вздовж ланки від точки ;

Сила реакції на кривошип зі сторони ланки 4 - прикладена в точці С₁ і направлена протилежно визначеній силі ;

Сила реакції на кривошип зі сторони стійки , прикладена в точці О₂ (силу направляємо довільно, бо вона - невідома);

Врівноважуючи сила прикладаємо в точці С₁ і направляємо перпендикулярно кривошипу.

Визначаємо величину зрівноважуючої сили, склавши рівняння моментів відносно точки О₂:

Тоді:

Визначаємо реакцію для чого складаємо векторне рівняння для сил, що діють на ланку 1:

Масштаб

• для 1-го положення:

• для 10-го положення: