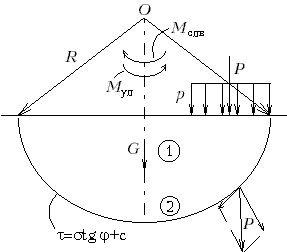
Яка основна ідея покладена в основу методу круглоциклічних поверхонь?
В основі цього методу закладена ідея про те, що при руйнуванні основи під фундаментом виникають дві тверді неграничні області, що відділяються друг від друга круглоциліндричною поверхнею (рис.М.12.14). При граничних умовах одна (верхня) область 1 сковзає уздовж цієї поверхні по іншій нижній області 2. Завдяки умові, що обидві області тверді, можливе здійснення переносу діючих сил уздовж ліній їхньої дії й оперирование рівнодіючими. Найнебезпечніша круглоциліндрична поверхня перебуває шляхом пробного пошуку й визначення мінімальної величини відносин моменту всіх утримуючих сил до моменту сил, що зрушуються.
|
Рис.М. 12.14. Схема для розрахунку граничного навантаження в припущенні утворення круглоциліндричних поверхонь ковзання |
Які рівняння задовольняються і які не задовольняються в способі круглоциліндричних поверхонь?
У способі круглоциліндричних поверхонь повністю не задовольняються умови рівноваги для проекцій на осі (вертикальну й горизонтальну), тому що нормальна стосовно дуги окружності складова рівнодіючого навантаження множиться на коефіцієнт внутрішнього тертя й цим вона переводиться в дотичний компонент, у той час як фактично уздовж поверхні мобілізується не все тертя, а тільки частина його. Те ж саме робиться й із силами зчеплення, що діють уздовж потенційної поверхні ковзання, які мобілізуються лише частково. Тому цей спосіб варто розглядати як інженерний і недостатньо твердий.
Який вид має формула для коефіцієнта запасу (надійності)? Чи залежить коефіцієнт запасу стійкості на зрушення від радіуса окружності ковзання?
Ця формула для способу круглоциліндричних поверхонь має такий вигляд:
.
Від радіуса відношення моментів сил, що входять у цю формулу, формально не залежить, однак коли відшукується мінімальне значення величини Kзап= n, то встановлюються й радіус, і положення центра дуги, що відповідають умові цього мінімуму.
Яким чином розраховується стійкість на зрушення по площині контакту спорудження з основою?
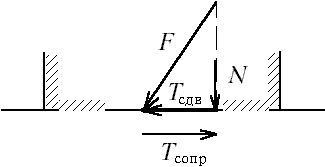
Якщо не враховується величина відсічі ґрунту з боку, куди спрямоване зрушення, то підраховується вертикальна складова діючих сил N (рис. М. 12.17), потім вона множиться на коефіцієнт тертя f і додаються сили зчеплення по контакті C. Після цього максимально можливе значення, що вийшло, сили опору ділиться на величину сили, що зрушує, Tсдв і тим самим перебуває величина коефіцієнта запасу (надійності) , тобто
.
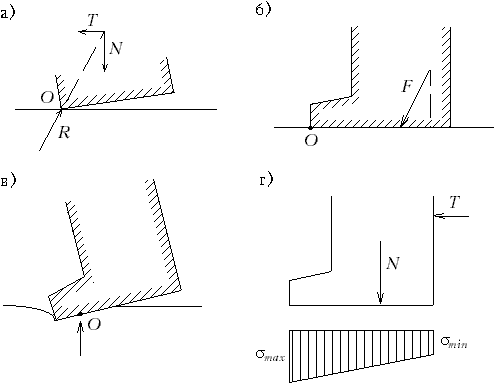
Яким чином розраховується стійкість спорудження на перекидання?
Стійкість на перекидання (рис.М.12.18,а) оцінюється по відношенню моментів сил утримуючих і сил перекидаючих, узятих щодо крайньої точки. При цьому вважається, що спорудження як би ледве піднялося й тому реакція основи у вигляді зосередженої сили прикладена в крайній точці, а, отже, в умову рівноваги моментів вона не ввійде, тому що проходить через цей полюс.
Для того, щоб збільшити стійкість на перекидання, варто ввести ліворуч у спорудження консоль (рис.М.12.18,б). У випадку деформування основи обертання при перекиданні відбувається не навколо однієї крайньої точки, а спорудження "входить" у ґрунт основи, тому й обертання відбудеться навколо центра, що розташовується в межах підошви спорудження (рис.М.12.18,в). Перекиданню передує крен спорудження. Звичайно прагнуть не допускати відриву підошви від ґрунту, крім особливих випадків (наприклад, дії сейсмічних сил), і обмежувати співвідношення між максимальними й мінімальним вертикальними напругами (рис.12.18,г). При встановленні величин цих максимальних напруг варто враховувати також і дотичні зусилля, що виникають по підошві спорудження.
|
Рис.М. 12.18. Схема для розрахунку стійкості на перекидання: а - перекидання відбувається навколо точки O; б - консоль, що збільшує опір перекиданню; в - перекидання навколо точки O при вдавленні спорудження в основу; г - епюра нормальних напруг по підошві фундаменту |
ТЕОРІЯ ГРАНИЧНОЇ РІВНОВАГИ ГРУНТІВ
Яким чином записується умова граничної рівноваги в головних напругах? Яким чином ця умова перетвориться в залежність, у яку входять всі три компоненти напруг (у декартових координатах)?
Умова граничної рівноваги в головних напругах має вигляд
За допомогою кола Мора й теореми Пифагора, відповідно до якої
а
також з огляду
на, що
одержимо
наступну умову:
Скільки невідомих компонентів напруг ми маємо у випадку плоскої задачі, осиметричної задачі, просторової задачі в загальному випадку?
У випадку плоскої задачі ми маємо три невідомих компоненти напруг, у випадку осиметричної задачі чотири, а для просторової задачі в загальному випадку шість компонентів напруг.
Які додаткові залежності залучаються до рівнянь рівноваги в теорії граничної рівноваги сипучого середовища в плоскій, осиметричній і просторовій задачах і скільки цих додаткових залежностей?
До двох рівнянь рівноваги у випадку плоскої задачі залучається одна умова, що зв'язує компоненти напруг, умова граничної рівноваги. У випадку осимметричної задачі до двох рівнянь рівноваги (проекції на осі координат) залучається також одна умова граничної рівноваги, а додатковим, оскільки компонентів у рівняннях чотири, є умова рівності між собою двох головних напруг (проміжне дорівнює мінімальному або максимальному). У випадку просторової задачі ми маємо три рівняння рівноваги й одне рівняння граничної рівноваги - таким чином, не вистачає двох рівнянь.
У яких випадках загальна система рівнянь теорії граничної рівноваги є замкнутої? У яких випадках і скільки рівнянь не вистачає для одержання замкнутості системи? Що називається умовою "повної" і "неповної" сипкості?
У випадку плоскої задачі система виявляється повністю замкнутою. У випадку осиметричної задачі не вистачає одного рівняння й залучається умова "повної сипкості" шляхом прирівнювання проміжної головної напруги мінімальному або максимальному, після чого система стає замкнутою. Якщо не залучити цієї умови, то система буде незамкнутою (неповною). У випадку просторової задачі не вистачає двох рівнянь і система виявляється незамкнутою.
Чому дорівнює порядок системи диференціальних рівнянь у частинних похідних? Який порядок має система диференціальних рівнянь теорії пружності (плоска задача) і теорії граничної рівноваги сипучого середовища?
Порядок системи диференціальних рівнянь у частинних похідних дорівнює сумі порядків вхідних у неї рівнянь. Система диференціальних рівнянь теорії пружності має четвертий порядок, а система рівнянь теорії граничної рівноваги другий порядок, тому що рівняння граничної рівноваги включає тільки компоненти напруг, але не їхні похідні. Це рівняння другого ступеня, але нульового порядку.