5. Условная вероятность и ее свойства. Правило и теорема умножения вероятностей.
Информация о наступлении одного события может повлечь изменение шансов появления другого.
П
усть
- конечное пространство равновозможных
элементарных исходов.
– некоторые события. Вероятность, того,
что событие
произойдет равно
,
если же известно, что событие
произошло, то следует выбрать новое
вероятностное пространство
,
и рассматривать событие
.
Т.о. вероятность того, что событие
произойдет, при условии, что
уже произошло:
.
Полученное выражение
для
и принимается за определение условной
вероятности.
Опр Пусть
- некоторое вероятностное пространство
,
.
Условной вероятностью события
,
при условии, что
уже произошло называется величина:
.
Условная вероятность при фиксированном удовлетворяет всем аксиомам вероятности, а именно:
(аксиома
неотрицательности);
(аксиома
нормированности);
.
Т.к.
.
Из справедливости этих аксиом, можно утверждать, что условная вероятность обладает всеми свойствами вероятностей.
Из определения условной вероятности вытекает правило умножения вероятностей:
,
.
Обобщим правило умножения на случай счетного числа событий (теорема умножения):
.
6. Независимость событий. Свойства независимых событий. Независимость в совокупности.
События являются независимыми, если появление одного из этих событий не меняет вероятности другого.
Опр Говорят,
что событие
не зависит от
,
если
,
иначе события зависимы.
Покажем, что понятие независимости является симметричным: пусть , тогда
.
В силу симметрии говорят, что события и независимы.
Из правила умножения
вытекает следующее симметричное
определение независимых событий: события
и
независимы, если
- вероятность факторизуется.
Свойства независимых событий:
Если и независимы, то независимыми являются также и
,
и
,
и
.
.
Остальное доказывается аналогично.
Если не зависит от
и
,
которые являются несовместимыми, то
не зависит от
.
.
Если рассматривать более 2-х событий вводится понятие независимости в совокупности:
Пусть
- некоторые события на вероятностном
пространстве
.
События
называются независимыми в совокупности,
если
:
.
Для
получим, что независимость из независимости
в совокупности следует попарная
независимость, обратное утверждение
не верно.
7. Формулы полной вероятности и Байеса. Пример.
Пусть
- ПГС, причем
и
- известны
.
Найдем
.
- слагаемые справа
попарно несовместны
с
учетом аддитивности вероятности и
правилом умножения получим:
- формула полной
вероятности.
- гипотезы, отметим,
что
,
т.к. гипотезы составляют ПГС.
Пусть
с экспериментом связано
- гипотез, вероятности которых известны,
также известно, что гипотеза
сообщает событию
вероятность
.
Предположим, что после проведение
эксперимента событие
произошло. Этот факт приводит к переоценке
первоначальных вероятностей гипотез
.
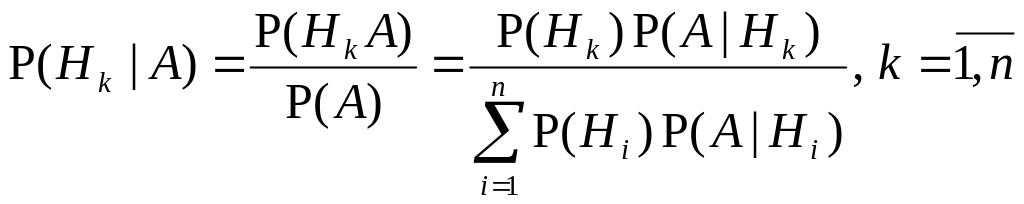- формула Байеса,
где
- априорные вероятности гипотез;
- апостериорные
вероятности гипотез.
Пример:
По
каналу связи с помехами передаются
бинарные символы (0 и 1). Вероятность
искажения символа в канале равна
.
Вероятности символов на входе каналов:
и
.
На выходе принят сигнал соответствующий
.
Какова вероятность того, что на входе
также была
.
Решение:
.
Т.о. необходимо найти апостериорную
вероятность
.
Очевидно,
и
.
По формуле Байеса получим:
;
.