"Теория вероятностей и математическая статистика"
1. Случайный эксперимент. Пространство элементарных событий. Случайные события и операции над ними.
Эксперимент результат которого может измениться при сохранении условий проведения и непредсказуемым образом называется случайным экспериментом (СЭ).
Всякий факт, который может произойти в результате случайного эксперимента, называется случайным событием (явлением) (СЯ).
Примеры:
СЭ являются: подбрасывание монеты,
игральной кости, 2-х монет, подбрасывание
монеты до выпадения герба, стрельба по
мишени (исход – попадание в точку
,
т.о. множество его исходов не счетное).
1. СЯ, рассматриваемые в ТВ, могут наблюдаться неограниченное число раз, притом в неизменных условиях.
2. СЯ должны обладать свойством статистической устойчивости частот.
Опр
Множество
всех возможных взаимоисключающих
исходов СЭ называется пространством
элементарных событий.
Элементы множества
называются элементарными событиями и
обозначаются
.
О
пр
Подмножества
называются случайными
событиями
(СС) и обозначаются
.
Говорят, что в результате эксперимента
произошло событие
,
если в эксперименте произошел один из
элементарных исходов, входящих в
.
Введем операции над СС:
Сумма
- состоит из всех элементарных исходов
или
.П
роизведение
- состоит из всех элементарных исходов
и
и
.
Операции суммы и произведения обобщаются на любое конечное или счетное число событий:
- сумма;
- произведение.
Разность
Противоположное событие
- достоверное
событие (происходит всегда в результате
эксперимента). Событие
не содержит ни одного элементарного
исхода и называется невозможным.
Говорят, что событие
влечет
(или
следует из
)
,
если все элементарные исходы
событию
.
События
(равносильны), если
и
.
События
и
,
которые не могут произойти одновременно,
т.е.
называются несовместными.
Говорят, что события
образуют полную группу событий (ПГС),
если они попарно несовместны (т.е.
)
и
.
Свойства операций над событиями:
Коммутативность:
.Ассоциативность:
.Дистрибутивность:
.
.
.
.
.
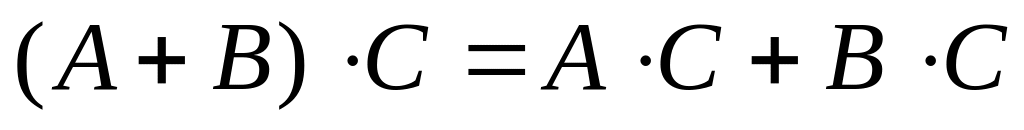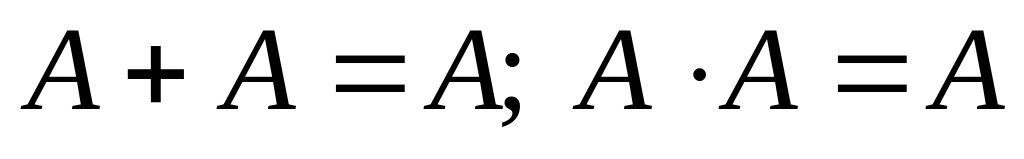- з-ны де Моргана.
,
то
.
2. Классическое определение вероятности (ков). Урновая схема. Пример.
Говорят, что СЭ удовлетворяет КОВ, если:
1.
2. Исходы случайного эксперимента равновозможные.
Исходы можно считать равновозможными, если они обладают свойством симметричности относительно условий проведения экспериментов (т.е. ни один исход не имеет предпочтение перед другим).
Пусть
и
- благоприятствующее событие и
.
Согласно КОВ, за
принимают отношение числа исходов,
благоприятствующих
к общему числу исходов:
.
Свойства, вытекающие из классического определения вероятности:
1.
;
2.
- условие нормировки;
3.
;
.
4.
т.к.
.
5.
из свойства 4 (
).
6.
.
.
Покажем несовместность событий
и
:
.
Тогда
.
7.
т.к.
и свойство 6.
Рассмотрим
урновую схему:
В урне содержится
шаров, из которых
- белых. Наугад из урны извлекается
шаров. Какова вероятность того, что
среди них окажется ровно
белых?
Р
.
Число благоприятных исходов:
.
.
Пример: В партии из 100 деталей содержится 5 бракованных. Для контроля наугад отбирают 10 деталей. Какова вероятность того, что среди них окажется хотя бы 1 бракованная.
Решение:
Рассмотрим событие
,
тогда
и
.
Получим
.