Вопрос 27: Средняя гармоническая и ее свойства.

Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.

Формула средней геометрической взвешенной применяется в тех случаях, когда статистическая информация не содержит частот f по отдельным вариантам х совокупности и представлена как их произведение xf. Для того чтобы исчислить среднюю геометрическую, необходимо обозначить: xf = w, откуда f = w/x.

Преобразуем формулу средней арифметической так, чтобы по имеющимся данным х и w можно было вычислить среднюю. В формулу средней арифметической взвешенной вместо xn подставим w, а вместо n — отношение w/x и таким образом получим формулу средней гармонической взвешенной:

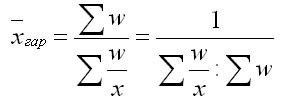
Средняя гармоническая простая применяется в тогда, когда вес каждого варианта равен единице. Она вычисляется по формуле:

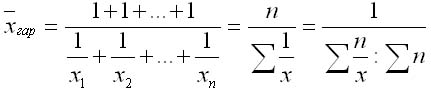
где 1/x - отдельные варианты обратного признака, встречающиеся по одному разу; n — число вариантов.

Вопрос 28: Понятие вариации признака

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Колебания отдельных значений характеризуют показатели вариации.

Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.

Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.

Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (Хмах) и наименьшим (xmjn) значениями вариантов:

Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений.

Меру вариации более объективно отражает показатель дисперсии.

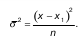
Среднее квадратическое отклонение – это мерило надежности средней.

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах, которые позволяют сравнивать характер рассеивания в различных распределениях. Расчет показателей меры относительного рассеивания осуществляют отношением абсолютного показателя рассеивания к средней арифметической и умножают на 100%.

При помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку-фактору, можно определить три показателя колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внутригруп-повых дисперсий.

Общая дисперсия характеризует вариацию признака, зависящую от всех условий в изучаемой статистической совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки, характеризует колеблемость групповых (частных) средних хi и общей средней хо.

Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе, возникает под влиянием факторов кроме положенного в основу группировки.

Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им.