
- •Вопрос 1: Предмет и метод статистики
- •Вопрос 2: История статистики
- •Вопрос 3: Задачи статистики
- •Вопрос 4: Принципы организации государственной статистики рф
- •Вопрос 5: Понятие и сущность статистического наблюдения
- •Вопрос 6: Организация статистического наблюдения
- •Вопрос 7: Основные организационные формы статистического наблюдения
- •Вопрос 8: Ошибки статистического наблюдения и способы их устранения
- •Вопрос 9: Понятие сводки и группировки статистических данных
- •Вопрос 10: Основное содержание и задачи статистической сводки
- •Вопрос 11: Сущность и классификация группировок
- •Вопрос 12: Основные правила построения статистических таблиц
- •Вопрос 13: Организационные формы статистического наблюдения (похож на 7 вопрос!)
- •Вопрос 14: Виды и способы статистического наблюдения
- •Вопрос 15: Программно-методологические и организационные вопросы статистического наблюдения
- •Вопрос 16: Статистические таблицы
- •Вопрос 17: Основные правила составления таблиц
- •Вопрос 18: Графическое изображение рядов распределения
- •Вопрос 19: Классификация статистических графиков
- •Вопрос 20: Общие принципы построения статистических показателей
- •Вопрос 21: Абсолютные величины.
- •Вопрос 22: Относительные величины
- •Вопрос 23: Виды Относительных величин
- •Вопрос 24: Сущность и значение средних величин
- •Вопрос 25: Виды средних величин и способы их вычисления.
- •Вопрос 26: Средняя арифметическая и ее свойства.
- •Вопрос 27: Средняя гармоническая и ее свойства.
- •Вопрос 28: Понятие вариации признака
- •Вопрос 29: Абсолютные показатели вариации
- •Вопрос 30: Относительные показатели вариации
- •Вопрос 31: Ряды динамики и их виды
- •Вопрос 32: Правила построения рядов динамики
- •Вопрос 33: Показатели анализа рядов динамики
- •Вопрос 34: Понятие индексов
- •Вопрос 45: Дисперсия: сущность и порядок расчёта
- •Вопрос 46: Основные свойства дисперсии Свойства дисперсии
- •Вопрос 47: Показатели абсолютного прироста и порядок их исчисления
- •Вопрос 48: Порядок исчисления агрегатных индексов
- •Вопрос 49: Порядок исчисления агрегатного индекса Пааше
- •Вопрос 50: Понятие и виды корреляционного анализа
- •Вопрос 51: Методы регрессионного анализа
- •Вопрос 52: Выборочное наблюдение: виды и схемы отбора
- •Вопрос 53: Принципы построения группировок
- •Вопрос 54: Основные элементы статистического графика
Вопрос 25: Виды средних величин и способы их вычисления.
Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая.
В изучении средних величин применяются следующие показатели и обозначения.
Признак, по которому находится средняя, называется осредняемым признаком и обозначается х; величина осредняемого признака у любой единицы статистической совокупности называютиндивидуальным его значением, или вариантами, и обозначают как хл, х2, x3,... хп; частота – это повторяемость индивидуальных значений признака, обозначается буквой f.
Один из наиболее распространенных видов средней – средняя арифметическая, которая исчисляется тогда, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.
Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной.
Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f.
Средняя гармоническая взвешенная, тождественна средней арифметической: Когда произведения fxодинаковы или равны
единицы (m= 1) применяется средняя гармоническая
простая:
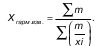
где х– отдельные варианты; n– число.
Если имеется n коэффициентов роста, то формула среднего коэффициента:
![]()
Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.
Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.
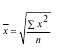
Средняя квадатическая взвешенная равна:
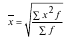
Вопрос 26: Средняя арифметическая и ее свойства.
Средняя арифметическая – самый распространенный вид средней величины. Когда речь идет о средней величине без указания ее вида, подразумевается именно средняя арифметическая. Она исчисляется в тех случаях, когда объем усредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. Например, общий фонд заработной платы – это сумма заработных плат отдельных работников, общее число рабочих в промышленности – это сумма их численностей на отдельных промышленных предприятиях, общий сбор урожая – сумма урожаев с каждого гектара площади и т.д.
Свойство 1. Если каждую варианту совокупности уменьшить или увеличить на какое-то произвольное положительное число А, то и средняя арифметическая уменьшится или увеличится на столько же.
Упражнение 1. Доказать свойство 1.
Свойство 2. Если каждую варианту разделить или умножить на одно и тоже число А, то и средняя арифметическая изменится во столько же раз.
Упражнение 2. Доказать свойство 2.
Свойство 3. Сумма произведений отклонений вариант от их средней арифметической на соответствующие им частоты равна нулю.
Упражнение 3. Доказать свойство 3.
Свойство 4. Сумма квадратов отклонений вариант от их средней арифметической меньше суммы квадратов отклонений тех же вариант от любой другой величины А, не равной средней арифметической.
