8. Оценивание параметрических моделей. Метод спектрального анализа.

Этот раздел описывает методы, которые оценивают частотные характеристики и спектры непосредственно. Функция R_yu() взаимной ковариации между y(t) и u(t) определен как Ey(t-)u(t). Перекрестный спектр Ф_yu(u) определен. При условии, что вход u(t) независим от v(t), подразумеваются следующие отношения между спектрами.

(44)

Оценивая различные вовлеченные спектры, функция частоты и спектр шума могут быть оценены следующим образом. Формы оценки функций ковариации , и , используют

(45)

и аналоговые выражения для других функций. Сформированы оценки соответствующих спектров

(46)

и аналогичное выражение для и , где - так называемое окно задержки, и М - ширина окна задержки. Оценки тогда сформированы как

, (47)

эта процедура известна как спектральный анализ.

9. Оценивание параметрических моделей. Метод прогноза ошибки (рем).

10. Идентификация с помощью регрессионных методов. Статическая задача для системы с одним выходом.

Регрессионный анализ является в настоящее время класси­ческим статистическим методом. Благодаря своим широким возможностям различные регрессионные процедуры давно и ус­пешно используются в инженерной практике для идентификации процессов многомерных систем в реальном масштабе времени.

Методы идентификации, основанные на регрессионных про­цедурах с использованием метода наименьших квадратов, применимы как к линейным, так и к нелинейным процессам в реальном масштабе времени, посколь­ку они основаны на измерениях входных и выходных сигналов, которые можно получить в процессе нормального функциониро­вания системы.

В течение периода, пока выполняются измерения для регрес­сионной идентификации, параметры идентифицируемого процес­са принимаются стационарными или квазистационарными. Этот период должен быть не менее тТ, где Т — интервал измерения, a m — число идентифицируемых параметров. Если требуется идентифицировать m коэффициентов в п сов­местных уравнениях вида

x_j= a_0j + a_1j u₁+ a_2ju₂+ ...+ a_mju_m, j = 1, 2, ..., п, (1.1)

и если одни и те же u_i (i = l, 2, ... , m) присутствуют во всех п yравнениях, то все a_ij i,j могут быть идентифицированы за m+1 интервалов измерения. Следовательно, идентификация всех m коэффициентов этих п уравнений может проводиться од­новременно.

Для применения регрессионных методов требуется накопление данных о неустановившихся состояниях входа/выхода по меньшей мере на m+1 измерительных интер­валах. Следовательно, на i-м интервале времени регрессионная идентификация основывается на данных от (i-m-р)-го (р 0) до i-гo интервала. Аналогично на (i+1)-м интервале она базируется на данных от (i-m-р+1)-го до (i+l)-гo интервала, облегчая тем самым выявление нестационарности входных и выходных сигналов. Если необходимо идентифицировать более одного параметра, то для получения параметров регрессии требуется обращение матриц. Рекуррентный вид регрессионных методов, позволяющий обойтись без обращения матриц, обсуждается в следующем разделе. Регрессионные методы рассматриваются в связи с использованием методов квазилинеаризации в задачах идентификации, для идентификации с прогнозом и применительно к идентификации параметров устройства прогноза (предсказателя).

Статическая задача для системы с одним выходом

Рассмотрим линейную статическую систему, представленную на рис. 1.1, имеющую m входов U₁, ..., U_m и один выход X.

Рис. 1.1. Процесс с одним выходом.

Эта система может быть описана следующим линейным уравнением:

X = a₀ + a₁U₁ + a₂U₂ +...+ a_mU_m. (1.2)

Используя серию измерений величин X, U_j (j = 0, 1, 2, ..., m) в r моментов времени, можно определить параметры а_i следующим образом. Сначала вводят в память ЦВМ все r совокупностей измерений величин X и U_j. Далее эти r совокупностей измерений используют для вычисления и , где — среднее значение X, а — среднее значение U для указанной серии измерений. Обозначим

, (1.3)

. (1.4)

При этом уравнение (1.1) принимает вид

x = a₁u₁ + a₂u₂ +...+ a_mu_m. (1.5)

или в векторной форме

x = u^T a, (1.6)

где u, a — вектор-столбцы с элементами u_j, a_j соответственно. Поэтому r последовательных измерений удовлетворяют соотношениям

(1.7)

где  обозначает момент измерений х, u^T ( = 1, 2, ..., r). Определим далее вектор  и матрицу U следующим образом:

(1.8)

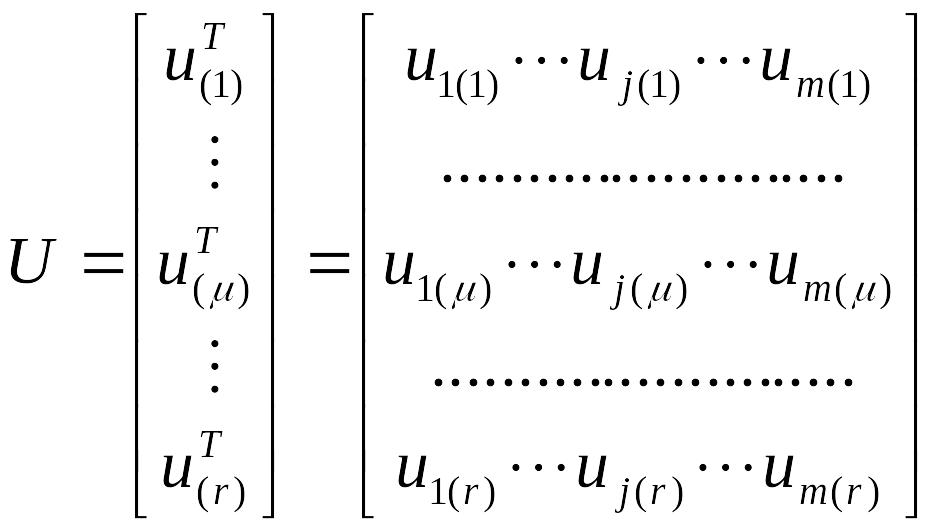. (1.9)

Следовательно, система уравнений (5.7) может быть записана в векторной форме:

. (1.10а)

Предполагая, что компоненты вектора  в уравнении (1.10а) являются оценками истинного вектора а, можно с помощью уравнения (1.10а) получить такие оценки вектора , что

=U (1.10б)

Скалярную сумму S квадратических ошибок оценивания можно определить следующим образом:

S = (-U )^T (-U )= tr [(-U )(-U )^T ], (1.11)

где tr [...] обозначает след матрицы [...]. Таким образом, наилучшая (в смысле наименьших квадратов) оценка вектора а должна удовлетворять соотношению

, (1.12)

или в векторной форме

. (1.13)

В соответствии с правилами вычисления следа матричной функ­ции, уравнение (1.13) преобразуется к виду

(1.14)

Поэтому наилучшая в смысле наименьших квадратов оценка вектора а удовлетворяет уравнению

, (1.15)

так что

, (1.16)

что и позволяет построить процедуру идентификации вектора а на основе линейной регрессии и метода наименьших квадратов. Отметим, что матрица (U^TU)^T существует только тогда, когда матрица U не является особенной.

Далее потребуем, чтобы число измерений r было больше чис­ла идентифицируемых параметров (r>>m). Если r = m, то в оценке  шум измерений не будет сглажен. Из этого условия сле­дует, что для адекватной идентификации требуется по крайней мере m+1 измерений, причем в течение этого периода система предполагается стационарной.

11. Параметрическая идентификация с функционалом метода наименьших квадратов (МНК)

12. Градиентный метод идентификации динамических систем (для дискретных и непрерывных систем управления)

13. Модели авторегрессии, используемые в MATLAB. Модель Бокса – Дженкинса.

Так называемая модель Бокса – Дженкинса (BJ):

(полиномы B(z), F(z), C(z) определены ранее, а D(z) = 1 + d₁z ^-1 + d₂z ^-2 +...+d_nd z ^{– nd}).

Данные модели можно рассматривать как частные случаи обобщенной параметрической линейной структуры

,

при этом все они допускают расширение для многомерных объектов (имеющих несколько входов и выходов).

14. Модели авторегрессии, используемые в MATLAB. Модель «вход – выход».

Модель «вход – выход» (в англоязычных источниках такая модель называется «Output-Error», то есть «выход-ошибка», сокращенно OE):

,

где F(z) = 1 + f₁z ^-1 + f₂z ^-2 +...+f_nf z ^{– nf}.

15. Модели авторегрессии, используемые в MATLAB. ARMAX модель.

ARMAX – модель (AutoRegressive-Moving Average with eXternal input – модель авторегрессии скользящего среднего):

A(z) y(t)= B(z) u(t - nk) + C(z) e(t),

где nk – величина задержки (запаздывания), C(z) = 1 + c₁z ^-1 + c₂z ^-2 +...+c_ncz ^{– nc}.

16. Модели авторегрессии, используемые в MATLAB. ARмодель.

Модели авторегрессии. Модель авторегрессии AR (AutoRegressive) считается самым простым описанием:

A(z) y(t)= e(t),

где A(z) = 1 + a₁z^-1 + a₂z^-2 +...+a_naz^-na.