3. Задачи идентификации стохастических систем

Процедура идентификации системы порождает следующую естественную логику действия: (1) собрать данные; (2) выбрать мно­жество моделей; (3) выбрать наилучшую в этом множестве модель. Однако вполне вероятно, что первая из так найденных моделей не выдержит проверки на этапе под­тверждения. Тогда нужно вернуться и пересмотреть различные шаги процедуры.

Рис. 1.8. Контур идентификации системы

Существует несколько причин несовершенства моделей:

1. численный метод не позволяет найти наилучшую по выбранному критерию модель;

2. критерий выбран неудачно;

3. множество моделей оказалось неполноценным в том смысле, что в этом мно­жестве вообще нет "достаточно хорошего" описания системы;

4. множество данных наблюдений не было достаточно информативным для того, чтобы обеспечить выбор хороших моделей.

По существу, главным в приложениях идентификации является итеративное ре­шение всех этих вопросов, особенно третьего, на основе априорной информации и результатов предыдущих попыток. См. рис. 1.11. Очевидно, что важным инструмен­тальным средством решения этой итеративной задачи является диалоговое програм­мное обеспечение.

4. Регрессионная идентификация линейных динамических процессов

5. Идентификация статики детерминированного объекта

6. Идентификация объекта при наличии случайных помех

7. Оценивание параметрических моделей. Метод корреляционного анализа.

Оценивание параметрических моделей (метод прогноза ошибки — Рrеdictive Error Method, сокращенно РЕМ) заключается в следующем. Пусть модель исследуемого объекта имеет вид так называемой обобщенной линейной модели

y(t)= W(z) u(t)+ v(t),

при этом шум v(t) может быть представлен как

v(t)=H(z) e(t),

где e(t)— дискретный белый шум, H(z) - некоторый полином от z.

Из данных выражений следует, что

e(t) = H^-1(z) [y(t) - W(z) u(t)].

При выборе в качестве критерия (функции потерь) величины

оценки коэффициентов полиномов модели могут быть найдены в результате решения следующей оптимизационной задачи (в общем случае нелинейной)

.

Нахождение такого решения (различными численными методами нелинейной оптимизации), как правило, достаточно сложно и трудоемко.

Несколько иной подход может быть применен к модели ARX . Формируя фильтрованные версии входа и умножая модель на s(t-k), k = 1, 2..., na и u(t-nk+1-k), k = 1, 2..., nb и суммируя по t, шум в (3-14) может быть коррелирован и применен для определения динамики. Это дает метод инструментальной переменной, где s(t) – называется инструментом.

Заметим, что еще более сложной является подобная процедура оценивания параметров модели для переменных состояния.

Основную задачу идентификации, которую мы будем исследовать, иллюстрирует рис. 1.

Рис. 1. Задача идентификации линейной системы с внешними тестовыми воздействиями.

Для идентификации высокочастотной составляющей h(t) необходимо, чтобы w(t) был широкополосным сигналом, и определение h(t) с нулевой ошибкой требует, вообще говоря, бесконечной полосы сигнала w(t). Практически почти всегда удается подобрать пробное воздействие, спектр которого зна­чительно шире полосы пропускания системы. Поэтому мы не будем рассматривать ошибки, возникающие из-за ограниченности спектра источника входного шума, хотя сделать это совсем нетрудно. Наблюдению доступен только z(t) —искаженный шумом вариант выходного сигнала y(t), а не сам y(t).

Блок-схема корреляционного метода идентификации приведена на рис.2. Предполагается, что система функционирует достаточно длительное время, так что достигнуто стационарное состояние. В то же время влияние нормального функционирования системы на процесс идентификации не рассматривается. Шумы w (t) и v (t) предполагаются эргодическими гауссовскими с нулевыми средними значениями. Как станет ясно впоследствии, предположение о равенстве нулю математических ожиданий шумов очень существенно, и нужно внимательно следить за обеспечением равенства средних значений нулю (если они отличны от нуля, но известны, их влияние может быть устранено путем центрирования случайных процессов).

Рис. 2. Коррелятор в задаче идентификации

Усредненное по времени значение выхода коррелятора есть

, (25)

причем соотношения

х(t) = z(t) w(t- ), (26)

z(t)=y(t) + v(t), (27)

(28)

следуют сразу из рис. 1. и 2.

Как видно из (25) и (26), математическое ожидание выхода коррелятора с учетом эргодичности и определения R_wz() =  {w(t) z(t + )} есть

. (29)

Согласно (27), (28) и предположению о равенстве нулю среднего значения v(t), обозначив R_w() =  {w(t) z(t + )}, получаем

. (30)

Применяя преобразование Фурье, приходим к соотношению для взаимной спектральной плотности

R_wz (p) = h(p) R_w(p). (31)

Если полоса частот R_w(p) значительно шире, чем полоса h(p), то приближенно можно считать, что

R_wz(p) = kh(p), R_wz () = kh(), (32)

Это соотношение является точным, если w(t) — белый шум, так что, обозначив через _D дельта-функцию Дирака, можно записать

R_w() = R_w_D(), R_w(p) = R_w/2, (33)

и тогда при R_w = 1

R_wz(t) = {x_a(t)} = h(). (34)

Таким образом достигается полная идентификация систе­мы, если использовать N параллельных корреляторов, позволяющих измерять

R_wz(t_i) = h(_i), i == 1, 2, ... N. (35)

Отметим, что до сих пор никак не использовалось пред­положение о гауссовости сигналов, так что в качестве источников пробных сигналов можно было бы применять и негауссовские источники. Однако анализ погрешностей, к которому мы теперь переходим, существенно использует допущение о гауссовости. Для определения статистических характеристик ошибки идентификации удобно вычислить корреляционную функцию выходного сигнала мультипликатора:

. (36)

Воспользуемся свойствами момента четвертого порядка гауссовской случайной величины. Именно, если совместное распределение a₁, a₂, a₂, a₃ и а₄ гауссовское, то

. (37)

Использовав это соотношение в (36), получим

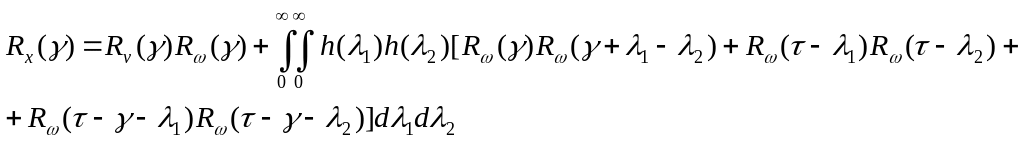(38)

Часть этого выражения представляет собой сигнал из (30). Остальные члены дают погрешность измерений.

Предполагая, что шум w(t) — белый, R_w () = R_w_D(), получим из (38)

(39)

Определив

, (40)

получим

(41)

Такова корреляционная функция шумовой компоненты x(t). Первый член этого выражения объясняется влиянием внешнего шума v(t). Два остальных возникают исключительно благодаря самой идентифицируемой системе и пробному сигналу. Доказано, что соответствующим выбором псевдослучайного пробного сигнала удается устранить влияние этих двух последних членов предыдущего соотношения. Как правило, именно эта ситуация и возникает во многих практических задачах идентификации, когда дисперсия помехи измерений значительно превосходит дисперсию пробного сигнала. При этом условии корреляционная функция шумовой составляющей x(t) равна

и представляет собой дисперсию x(t), вычисленную в предположении, что последние два слагаемых в (41) пренебрежимо малы. При этом мы сталкиваемся с задачей оценки постоянного сигнала

в присутствии гауссовского шума с нулевым средним и дисперсией

.

Тогда легко показать (Сейдж и Мелса [127]), что оптимальная оценка равна

.

Математическое ожидание выхода фильтра при этом равно R_h(). Если выход сглаживающего фильтра разделить на R_, его среднее значение будет h(), т. е. та самая весовая функция, которую мы пытаемся определить. Дисперсия ошибки идентификации при этом равна

.

По заданной дисперсии ошибки можно найти требуемую минимальную продолжительность процесса идентификации

.

Пример 3.3. Продемонстрируем различные источники ошибок, возникающих при идентификации, для случая h(t)=e^-а. Точное выражение для корреляционной функции выходного шума мультипликатора (41) примет вид

,

где

Ясно, что второй член в этом выражении меньше остальных, так что хорошим приближением может служить

.

Дисперсия ошибки идентификации убывает с ростом интервала наблюдений t. Учет «собственного шума», вносимого пробным сигналом, не приводит к существенным усложнениям. Снова можно использовать достаточно большое время наблюдений, выбирая R_w достаточно малым, чтобы шум не влиял на нормальную работу системы.

Как уже отмечалось, периодические псевдослучайные пробные воздействия часто оказываются предпочтительнее гауссовского шума, так как они легче генерируются, легче осуществляется задержка с помощью простых цифровых цепей задержки и умножение с помощью простых переключательных схем двоичной логики, а также благодаря тому, что двоичные сигналы имеют наиболее благоприятное отношение среднего квадрата входного сигнала к максимальной амплитуде на входе.