Приложение 1

Перечень вопросов для подготовки студентов к экзамену на 3 листах Идентификация систем

1. Представление линейных систем, наблюдаемость систем.

Система - это объект, в котором происходит взаимодействие между разнотипными переменными, и формируются наблюдаемые сигналы.

Интересующие нас наблюдаемые сигналы обычно называют выходными сигнала­ми. Все остальные сигналы называют возмущениями, причем возмущения могут быть разбиты на два класса: измеряемые непосредственно и доступные лишь косвен­ной оценке по воздействию, оказываемому ими на выходной сигнал. С точки зрения описания объекта разница между входными сигналами и измеряемыми возмущения­ми (помехами) часто оказывается несущественной. См. рис. 1.1.

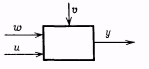
Рис. 1.1. Система с выходным сигналом у, входным сигналом u,

измеряемой помехой w и неизмеряемой помехой v.

Очевидно, что понятие системы сформулировано достаточно общо, поэтому не удивительна та важная роль, которую оно играет в современной науке. В рамках системного подхода решаются самые разнообразные задачи. Не пытаясь дать общего определения системы, проиллюстрируем это понятие на нескольких примерах.

Пример 1.1. Дом с солнечным подогревом

Принцип функционирования системы основан на том, что солнечные лучи разогревают воздух в солнечной панели, представляющей собой набор прозрачных трубок. Этот воздух подается в тепловой аккумулятор, в качестве которого используется заполненный камнями ящик. Накапливаемая тепловая энергия может использоваться для отопления дома. Интерес представляет вопрос, какое влияние оказывают на температуру аккумулятора изменения солнечного излучения и скорости поддува. Структурная системы изображена на рис. 1.3, а на рис. 1.4 показаны записи данных наблюдений в течение 16 часов. Замеры производились каждые 10 мин.

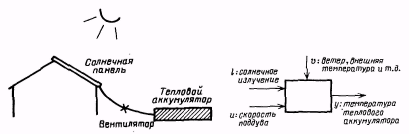
Рис. 1.2. Дом с солнечным подогревом Рис. 1.3. Система дома с солнечным

подогревом:

u - входной сигнал;

l - измеряемая помеха;

y – выходной сигнал;

v - неизмеряемая помеха;

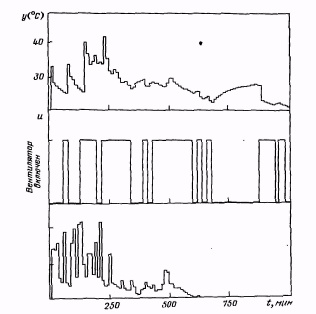
Рис. 1.4. Температура теплового аккумулятора y, скорость поддува u, интенсивность солнечного излучения l за 16-часовой отрезок времени. Интервал между замерами - 10 мин.

Наблюдатели

Во многих задачах теории систем и теории управления полное описание свойств помехи в уравнении (1) не используется. Вместо этого работают со свободной от шумов, или детерминированной, моделью:

y(t) = G(q)u(t). (27)

Однако в этом случае следует помнить, что уравнение (27) не отра­жает всех входо-выходных особенностей системы.

Конечно, модель (27) также можно использовать для "расчета", "выдвижения гипотез" и "прогнозирования" будущих значений выходного сигнала. Однако в от­сутствии модели шума остается свобода в выборе наилучшего способа употребле­ния модели (27). При этом ключевым моментом оказывается введение концеп­ции наблюдателей. Обычно эта концепция трактуется в терминах моделей в прост­ранстве состояний для описания (27).

Пример 2.3. Пусть

(28)

Это означает, что входо-выходное соответствие можно представить уравнением

, (29)

,

либо уравнением

. (30)

Теперь, если заданы описания (27) и (28) и данные у(s), и(s) (s t - 1) и требуется рассчитать возможное значение сигнала у(t), то можно воспользоваться формулой

(31)

или формулой

. (32)

Пока данные и описания системы правильны, между соотношениями (31) и (32) разни­цы нет: каждое из лих является "наблюдателем" (в нашем случае более уместно было бы говорить «предсказателем») системы. Возможность выбора между этими соотношениями может быть связана с дифференциацией степени их чувствительности к неточностям в данных и самих описаниях. Так, например, если нет данных о значениях входных и выходных сигналов до момента s = 0, то ошибка уравнения (31) является величиной, убывающей как a^t, а уравнение (32) при t  0 остается точным. Как только описание (27) дополняется моделью шума типа (1), выбор предсказателя становится единственным.