Билет 28.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: Па·с = 10 пуаз) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹−10¹² Па·с

Закон вязкости (внутреннего трения) Ньютона — математическое выражение, связывающее касательное напряжение внутреннего трения   (вязкость) и изменение скорости среды   в пространстве   (скорость деформации) для текучих тел (жидкостей и газов):

,

где величина   называется коэффициентом внутреннего трения или динамическим коэффициентом вязкости (единица СГС — пуаз); с физической точки зрения она представляет собой удельную силу трения при градиенте скорости, равном единице. Кинематическим коэффициентом вязкости называется величина   (единицаСГС — Стокс,   − плотность среды).

Закон Ньютона может быть получен аналитически приёмами физической кинетики, где вязкость рассматривается обычно одновременно с теплопроводностью и соответствующим законом Фурье для теплопроводности. В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где   — средняя скорость теплового движения молекул,   − средняя длина свободного пробега.

Большое каноническое распределение Гиббса.

, 101\* MERGEFORMAT (.)

где большая статистическая сумма и омега потенциал определены формулами:

202\* MERGEFORMAT (.)

Как и для канонического распределения энтропия задается формулой Больцмана.

303\* MERGEFORMAT (.)

Дифференциал омега потенциала должен соответствовать утверждению второго начала термодинамики.

404\* MERGEFORMAT (.)

При этом:

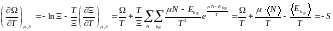505\* MERGEFORMAT (.)

606\* MERGEFORMAT (.)

707\* MERGEFORMAT (.)

Таким образом, мы получили утверждение второго начала термодинамики.

808\* MERGEFORMAT (.)

Среднее число частиц

909\* MERGEFORMAT (.)

продифференцируем по и убедимся, что

10010\* MERGEFORMAT (.)

задает флуктуацию числа частиц с системе, производная по температуре связана с соотношением

11011\* MERGEFORMAT (.)

с корреляцией и флуктуацией числа частиц.

Аналогично производные от средней энергии

12012\* MERGEFORMAT (.)

по и по 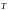соотношениями:

13013\* MERGEFORMAT (.)

с теми же величинами и флуктуацией энергии. Из этих четырёх соотношений легко выразить флуктуации и корреляцию энергии и числа частиц через производные аддитивных термодинамических величин по интенсивным параметрам.

14014\* MERGEFORMAT (.)

Поэтому

15015\* MERGEFORMAT (.)

и для макроскопических систем отклонения энергии и числа частиц от их средних значений пропорциональных ничтожно. Следовательно, в термодинамическом пределе большое каноническое распределение переходит в каноническое и микроканоническое.

Наконец заметим, что подобный аддитивный вид должен иметь и омега потенциал для однокомпонентной жидкости или газа , при этом, согласно 08, и

16016\* MERGEFORMAT (.)

К тому же результату можно придти и из 03, используя соотношения между термодинамическими потенциалами. Перепишем 03 в виде:

. 17017\* MERGEFORMAT (.)

Термодинамические соотношения для систем с переменным числом частиц.

Отвлекаясь от флуктуаций, под термодинамическими величинами следует понимать по определению( по физическому смыслу):

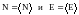18018\* MERGEFORMAT (.)

Из соотношения для энтропии 03 следует, что

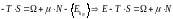19019\* MERGEFORMAT (.)

Но из определения свободной энергии следует, что

, 20020\* MERGEFORMAT (.)

и, согласно с 04-07

, 21021\* MERGEFORMAT (.)

поэтому получаем, что:

22022\* MERGEFORMAT (.)

Аналогичная добавка появляется в термодинамические выражения для дифференциалов других потенциалов.

. 23023\* MERGEFORMAT (.)

Из последней строчки следует уже известная нам формула 017, поскольку .