Билет 22.
В классической механике пространственные координаты и время являются независимыми (при отсутствии голономных связей, зависящих от времени), время является абсолютным, то есть течёт одинаково во всех системах отсчёта, и действуют преобразования Галилея. В релятивистской же механике события происходят в четырёхмерном пространстве, объединяющем физическое трёхмерное пространство и время (пространство Минковского) и действуют преобразования Лоренца. Таким образом, в отличие от классической механики, одновременность событий зависит от выбора системы отсчёта.
Основные законы релятивистской механики — релятивистское обобщение второго закона Ньютона и релятивистский закон сохранения энергии-импульса — являются следствием такого «смешения» пространственных и временной координат при преобразованиях Лоренца.
Сила
определяется как 
,
также известно выражение для релятивистского
импульса:
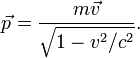
Взяв для определения силы производную по времени от последнего выражения, получим:
где
введены обозначения: 
и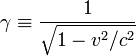 
.
В результате выражение для силы приобретает вид:
Отсюда видно, что в релятивистской механике в отличие от нерелятивистского случая ускорение не обязательно направлено по силе, в общем случае ускорение имеет также и составляющую, направленную по скорости.
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
— плотность жидкости,
— скорость потока,
— высота,
на которой находится рассматриваемый
элемент жидкости,
— давление в
точке пространства, где расположен
центр массы рассматриваемого элемента
жидкости,
— ускорение
свободного падения.
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли[2][3] или интегралом Бернулли[4][5].
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.
Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смыслкинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[6]).
Соотношение, близкое[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.
Для
горизонтальной трубы 
и
уравнение Бернулли принимает вид: 
.
Эта
форма уравнения Бернулли может быть
получена путём интегрирования уравнения
Эйлера для
стационарного одномерного потока
жидкости, при постоянной плотности
: 
.
Основным законом (уравнением) гидростатики называется уравнение[1]:
,
где
— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,
— плотность жидкости,
— ускорение свободного падения,
—
высота
точки над плоскостью сравнения
(геометрический напор[2]),
—
гидростатический напор[3].
Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.