Билет 21.

ЛАГРАНЖА УРАВНЕНИЯ

механики - обыкновенные дифференциальные уравнения 2-го порядка, описывающие движения механич. систем под действием приложенных к ним сил. Л. у. установлены Ж. Лаг-ранжем [1] в двух формах: Л. у. 1-го рода, или уравнения в декартовых координатах с неопределенными множителями Лагранжа, и 2-го рода, или уравнения в обобщенных лагранжевых координатах.

Л. у. 1-го рода описывают движения как голономных систем, стесненных только геометрич. связями вида   так и неголономных систем, на к-рые наложены, помимо связей (1), кинематич. связи вида 

где   - декартовы координаты и скорости точек, N - число точек системы, t - время,   - масса р- йточки, имеющей координаты. Связи   (1) и (2) предполагаются независимыми, т. е. ранги матриц   равны соответственно kи т.

Л. у. 1-го рода имеют вид 

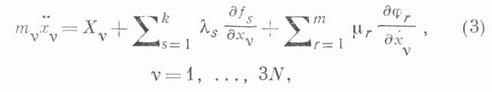
где   - неопределенные множители Лагранжа, пропорциональные реакциям связей,   - проекции на оси координат заданных активных сил, причем сила F_p действующая на р- юточку, имеет проекции 

К дифференциальным уравнениям (3) надлежит присоединить k+m уравнений (1) и (2), в результате чего получается система3N+k+т уравнений с таким же числом неизвестных   Л. у. 1-го рода на практике обычно применяются для систем с небольшим числом неизвестных.

Л. у. 2-го рода описывают движения лишь голономных систем, стесненных связями вида (1). Введением в рассмотрение n=3N-kнезависимых обобщенных лагранжевых координат q_i, с помощью к-рых любое возможное положение системы может быть получено при нек-рых значениях q_i из равенств 

обращающих уравнения (1) в тождества, устанавливается для каждого tвзаимно однозначное соответствие между возможными положениями системы и точками нек-рой области n-мерного конфигурационного пространства (q₁, .., q_n). В случае стационарных связей (1) всегда возможно выбрать переменные д;так, что время tне будет входить в уравнения (4). Далее записываются с помощью уравнений (4) выражения для суммы элементарных работ всех активных сил F_p на возможных перемещениях системы 

и кинетич. энергии системы 

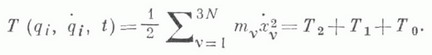
Здесь 

- обобщенная сила, соответствующая координате   - однородные степени s формы обобщенных скоростейq_i, причем 

В случае стационарных связей Т= Т ₂. Л. у. 2-го рода имеют вид 

Уравнения (5) представляют собой систему га обыкновенных дифференциальных уравнений 2-го порядка с неизвестными q_i. Они инвариантны по форме относительно выбора лагранжевых координат. Эта система уравнений движения имеет наименьший возможный порядок 2n. В этом, а также в отсутствии в уравнениях (5) реакций связей, состоит большое преимущество уравнений (5) по сравнению с Л. у. 1-го рода (3). После интегрирования системы (5) реакции связей могут быть определены из уравнений, выражающих второй закон Ньютона для точек системы.

В случае потенциальных обобщенных сил, когда существует силовая функция   такая, что   уравнения (5) принимают вид 

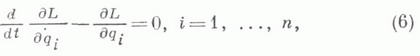
где   носит название функции Лагранжа, или кинетич. потенциала.

Если   или -  то уравнения (6) допускают обобщенный интеграл энергии 

или циклический интеграл 

соответствующий циклической координате q _а.

ОБОБЩЁННЫЕ КООРДИНАТЫ

       

независимые параметры qi (i=1, 2, ..., s) любой размерности, число к-рых равно числу s степеней свободы механич. системы и к-рые однозначно определяют положение системы. Закон движения системы в О. к. даётся s ур-ниями вида qi=qi(t), где t — время. О. к. пользуются при решении мн. задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число ур-ний, описывающих движение системы, по сравнению, напр., с ур-ниями в декартовых координатах (см. ЛАГРАНЖА УРАВНЕНИЯ В МЕХАНИКЕ). В системах с бесконечно большим числом степеней свободы (сплошные среды, физ. поля) О. к. являются особые функции пространственных координат и времени, наз. потенциалами, волн. функциями и т. п.