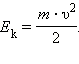Билет 13:

1. Работа и кинетическая энергия.

2. Силы инерции при ускоренном произвольном движении системы отсчета.

3. Парадокс Гиббса.

1. Работа и кинетическая энергия.

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Физическая величина, равная произведению модуля силы, действующей на тело, на модуль перемещения тела под действием этой силы и на косинус угла между направлением силы и перемещения, называется работой силы:  A = F ∙ S ∙ cos α.

Таким образом, работа силы равна изменению кинетической энергии тела:  A = ΔEk.

Это утверждение называется теоремой об изменении кинетической энергии тела.

Если тело движется по инерции, силы на него не действуют, работа не совершается и кинетическая энергия не изменяется.

Если на тело действует сила, но тело покоится, работа силы равна нулю.

Если на тело действует сила и тело движется, но угол между направлениями силы и перемещения равен 90°, работа силы также равная нулю.

В зависимости от величины угла между векторами перемещения и силы, работа силы может быть положительной и отрицательной.

Работа силы и кинетическая энергия – величины скалярные.

Чтобы получить единицу работы, надо в определяющее уравнение работы подставить единицы силы – 1 Н и перемещения – 1 м. Получаем: 1 Н∙м. Эта единица имеет собственное название – 1 джоуль (1 Дж).

2. Силы инерции при ускоренном произвольном движении системы отсчета. Движение в инерциальной со

Выполнив тривиальную математическую операцию в выражении третьего закона Ньютона (5) и перенеся член из правой части в левую, получаем безупречную математически запись:

(6)

С физической точки зрения, сложение векторов сил имеет своим результатом получение равнодействующей силы.

В таком случае, прочтённое с точки зрения второго закона Ньютона выражение (6) означает, с одной стороны, что равнодействующая сил равна нулю и, следовательно, система из этих двух тел не двигается ускоренно. С другой стороны здесь не высказаны никакие запреты на ускоренное движение самих тел.

Дело в том, что понятие о равнодействующей возникает лишь в случае оценки совместного действия нескольких сил на одно и то же тело. В данном же случае, хотя силы равны по модулю и противоположны по направлению, но приложены к разным телам и потому, касательно каждого их рассматриваемых тел по отдельности, не уравновешивают друг друга, поскольку на каждое из взаимодействующих тел действует лишь одна из них. Равенство (6) не указывает на взаимную нейтрализацию их действия для каждого из тел, оно говорит о системе в целом.^[12][13]

Материальная точка в двух декартовых системах координат: неподвижной O, считающейся инерциальной, и подвижной O'

Повсеместно используется запись уравнения, выражающего второй закон Ньютона в инерциальной системе отсчёта:

 (7)

Если   есть результирующая всех реальных сил, действующих на тело, то это выражение, представляющее собой каноническую запись Второго закона, является просто утверждением, что получаемое телом ускорение пропорционально этой силе и массе тела. Оба выражения, стоящие в каждой части этого равенства относятся к одному и тому же телу.

Но выражение (7) может быть, подобно (6), переписано в виде:

 (8)

Для постороннего наблюдателя, находящегося в инерциальной системе и анализирующего ускорение тела, на основании сказанного выше такая запись имеет физический смысл только в том случае, если члены в левой части равенства относятся к силам, возникающим одновременно, но относящимся к разным телам. И в (8) второй член слева представляет собой такую же по величине силу, но направленную в противоположную сторону и приложенную к другому телу, а именно силу  , то есть

 (9)

В случае, когда оказывается целесообразным разделение взаимодействующих тел на ускоряемое и ускоряющее и, чтобы отличить действующие тогда на основании Третьего закона силы, те из них, которые действуют со стороны ускоряемого тела на ускоряющее называют силами инерции   или «ньютоновыми силами инерции»^[12], что соответствует записи выражения (5) для Третьего закона в новых обозначениях:

 (10)

Существенно, что сила действия ускоряющего тела на ускоряемое и сила инерции имеют одно и то же происхождение и, если массы взаимодействующих тел близки друг другу настолько, что и получаемые ими ускорения сравнимы по величине, то введение особого наименования «сила инерции» является лишь следствием достигнутой договорённости. Оно так же условно, как и само деление сил на действие и противодействие.

Иначе обстоит дело, когда массы взаимодействующих тел несравнимы между собой (человек и твёрдый пол, отталкиваясь от которого он идёт). В этом случае деление тел на ускоряющие и ускоряемые становится вполне отчётливым, а ускоряющее тело может рассматриваться как механическая связь, ускоряющая тело, но не ускоряемая сама по себе.^[12]

В инерциальной системе отсчёта сила инерции приложена не к ускоряемому телу, а к связи.