10. Условие равной прочности зубьев колес и шестерни по напряжениям изгиба.

Условие равной прочности по напряжению изгиба

m≥267

Известно, что в условиях равной прочности геометрические размеры должны быть одинаковыми,

m₁=m_2; P₁=P_2; K_F1=K_F2; z₁n₁z₂n_2; YF ₁/[σ_F]₁= YF ₂/[σ_F]_{2 -} условие, обеспечивающее равную прочность

Тот из зубьев у которого отношение YF/[F] больше и есть менее прочный по напряжению изгиба. его и следует взять за основу при расчете m

Y_F – коэффициент формы зуба; z- количество зубьев; m- модуль; K_F – коэффициент расчетной нагрузки;

11 Косозубые цилиндрические колеса. Геометрические параметры. Силы действующие в косозубой передаче.

У косозубых колес зубья расположены не по образующей делительного цилиндра, а составляют с ней угол β

Профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба. Модуль в этом сечении должен быть так же стандартным. В торцевом сечении t-t или окружном направлении параметры косового зуба изменяются в зависимости от угла β:

• Окружной шаг p_t=p_n/cos β, Окружной модуль m_t=m_n/cos β, Диаметр делительной окружности d=m_tz=m_nz/cos β.

Силы действующие в косозубых передачах:

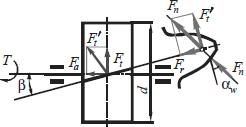
Здесь силу Fn раскладывают на три составляющие:

• Окружную силу Ft=2T/d

• Осевую силу Fa=Ft tg β

• Радиальную силу

• Нормальная сила

В косозубом цилиндрическом колесе линия контакта расположена наклонно, а нагрузка по линии контакта распределяется неравномерно. Наибольшая нагрузка наблюдается при зацеплении зубьев в средней части линии контакта в связи с тем, что в этом случае суммарная жесткость взаимодействующих зубьев наибольшая.

12. Прямозубое цилиндрическое колесо, эквивалентное косозубому. Вывод формулы для эквивалентного диаметра и числа зубьев. Расчет косозубой передачи на прочность по контактным напряжениям и по напряжениям изгиба.

Эквивалентным называется такое воображаемое прямозубое цилиндрическое колесо, форма и размеры зуба которого соответственно совпадают с формой и размерами зуба реального косозубого колеса в его нормальном сечении.

Нормальное сечение n–n косозубого колеса имеет форму эллипса с полуосями a и b'

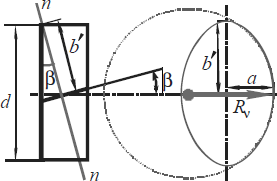
Радиус кривизны эллипса

диаметр эквивалентного колеса

число зубьев

по контактным напряжениям

Коэффициент повышения прочности

KHa – коэффициент учитывающий неравномерность распределения нагрузки ea – коэффициент торцевого перекрытия

значения ZНb в формуле предварительно оценивают приближенно; при некоторых средних значениях: b = 12°; ea = 1,5; KHa = 1,1, получим ZНb = 0,85.

или

по напряжениям изгиба.

YF – коэффициент формы зуба KF = KFβ*KFν – коэффициент расчетной нагрузки; b – ширина колеса; mn – модуль в нормальном сечении; ZFb – коэффициент повышения

прочности по напряжению изгиба

Yb – коэффициент учитывающий повышение изгибной прочности

при b > 40° принимают Yb = 0,7; Ea – коэффициент торцевого перекрытия, учитывает уменьшение нагрузки ввиду многопарности зацепления

13. Прямозубые конические колеса. Геометрические параметры. Силы действующие в прямозубой передаче.

Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом Σ. Наиболее распространены передачи с углом Σ = 90°.

dm – средний делительный диаметр. de – внешний делительный диаметр. Rm – среднее конусное расстояние. Re – внешнее конусное расстояние. b – ширина зубчатого венца. δ- углы делительных конусов

Силы:

В зацеплении К.П. действуют силы: окружная Ft, радиальная Fr и осевая Fa. По нормали к зубу действует сила Fn. Которая раскладывается на Ft и Fr’. В свою очередь Ft’ раскладывается на Fa и Fr.

• Ft=2T1/dm1, Fn=Ft/cos α,

• Fr’=Ft tg α

• Fr=Fr’ cos δ1=Ft tg α sin δ1,

• Fa=Ft’ sin δ1=Ft tg α sin δ1

Для колеса направление сил противоположно. При этом Fa является радиальной силой , а Fr- осевой.