7. Расчет зубьев прямозубых цилиндрических колес на контактную прочность. Вывод формулы для проектного расчета.

Допущения, мало влияющие на результаты расчетов практически для большинства используемых передач.

1. наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление. Поэтому расчет контактных напряжений принято выполнять для однопарного зацепления зубьев в полюсе.

2. Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами R1 и R2; здесь R1 и R2 радиусы кривизны эвольвентной поверхности зуба в полюсе зацепления.

Контактные напряжения определяют по формуле Г. Герца где Fn – нормальная сила в зацеплении 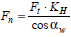где Ft – окружная сила; aw – угол зацепления; KH – коэффициент расчетной нагрузки, учитывающий реальные условия работы зубчатой передачи здесь соответственно KHb – коэффициент концентрации нагрузки по длине зуба, KHυ – коэффициент динамической нагрузки. Из кинематических характеристик известно, что зубчатая передача, выполненной без смещения dw i = di. 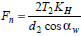где d1 и d2 – делительные диаметры зубчатых колес. Далее определим радиусы кривизны поверхности зубьев при зацеплении в полюсе в зависимости от параметров колеса и шестерни. Из треугольника ПА2О2 получим а из треугольника ПА1О1 тогда Выразим d1 через передаточное число u тогда 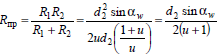получим где

В результате математических преобразований окончательно получим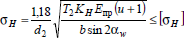

8. Выбор модуля зубчатой передачи.

В формулу для межосевого расстояния aw величина модуля m непосредственно не входит. Таким образом, величина aw, определяемая из условия контактной прочности, не зависит от m. Существует два основных способа определения модуля.

I способ

Экспериментально установлено, что рациональные значения модуля лежат в пределах

m = (0,01…0,02)aw, HB1,2 <= 350,

m = (0,0125…0,025)aw, HB1 > 350, HB2 <= 350,

m = (0,016…0,0315)aw, HB1,2 > 350.

II способ

Задаются числом зубьев на шестерни z1. Минимально число z1, при котором отсутствует подрезание зубьев: z1 > 17. Для снижения шума в зацеплении обычно задают z1 = 20 … 25 зубьев, соответственно z2 = z1*u.

Далее из зависимости d1 + d2 = m* z1 + m* z2 = 2aw получим m= 2aw /(z1+z2)

Полученное значение m округляем до ближайшего стандартного значения.

III способ

Вычисляем модуль m по формуле и округляем до большего стандартного значения.

9. Расчет зубьев и прямозубых цилиндрических колес на изгиб. Вывод формул для проверочного проектного расчета.

Наибольшие напряжения изгиба возникают у основания зуба в зоне перехода эвольвентной поверхности в галтель. Здесь же наблюдается концентрация напряжений. Допущения:

1. в зацеплении находится одна пара зубьев; 2. сила приложена к вершине зуба; 3. силами трения на поверхности зуба пренебрегаем; 4. радиальной силой Fr в расчете пренебрегаем 5. зуб рассматриваем как консольно закрепленную балку, для которой справедлива гипотеза плоских сечений.