Вариант 8.

Задача 1.

На предприятии выпускается три вида изделий, на которые используется три вида сырья.

Тип сырья	Нормы расхода сырья на одно изделие			Запасы сырья
	А	Б	В
I	1	2	1	430
II	3	0	2	460
III	1	4	0	420
Цена изделия	3	2	5

7. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 80 кг, а запасы сырья II вида уменьшить на 10кг?

8. Целесообразно ли выпускать изделие Г ценой 7 ед., если нормы затрат сырья на него составляют 2, 4 и 3 кг?

Построение математической модели задачи.

Введем следующие обозначения:

x₁ – количество изделий А;

x₂ – количество изделий Б;

x₃ – количество изделий В;

Прибыль от выпуска изделий А составляет 3x₁, изделий Б – 2x₂, изделий В – 5x₃.

Запишем критерий оптимальности:

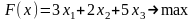
Ограничения имеют вид:

x₁+2x₂+x₃<= 430, ограничение по типу сырья I

3x₁+0x₂+2x₃<=460, ограничение по типу сырья II

x₁+4x₂+0x₃<=420, ограничение по типу сырья III

x₁>=0, x₂>=0, x₃>=0.

Решение задачи.

1. Выбор и указание адресов ячеек, в которые будет помещен результат решения (изменяемые ячейки).

В нашей задаче х₁, х₂, х₃ обозначают количество изделий каждого типа. Для оптимального значения вектора Х=( х₁, х₂, х₃) зарезервируем ячейки B2:D2, а для оптимального значения целевой функции (максимальная прибыль) – ячейку E4.

2. Ввод исходных данных.

Введем исходные данные, как показано на рисунке 1

Рис.1.

Для удобства чтения будущих отчетов Рисунок присвойте имена следующим ячейкам:

E7 – тип сырья I;

E8 – тип сырья II;

E9 – тип сырья III;

В4 – прибыль_1 изделия А;

С4 – прибыль_1 изделия Б;

D4 – прибыль_1 изделия В;

E4 – суммарная прибыль .

3. Ввод зависимости для целевой функции.

Поместите курсор в ячейку E4. С помощью мастера функций введите функцию СУММПРОИЗВ. В окне функции в строку Массив1 введите В2:D2 (ячейки искомых переменных). Этот массив будет использоваться при вводе зависимостей для ограничений, сделайте на него абсолютную ссылку с помощью клавиши E4.

В строку Массив2 введите B4:D4. На экране до нажатия кнопки ОК будем иметь

Рис. 2.

После нажатия кнопки ОК, то есть после выполнения функции СУММПРОИЗВ вид экрана показан на рисунке 3.

Напомним, что адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, адреса которых следует ввести.

Рис. 3.

4. Ввод зависимостей для ограничений.

Скопируйте формулу из ячейки E4 в ячейки E7:E9. Экран примет вид:

Рис. 4.

Проверьте введенные формулы в режиме просмотра формул (см. рисунок 5).

Рис. 5

5. Запустите команду Поиск решения. Появится диалоговое окно Поиск решения (рисунок6):

Рис. 6.

5. Установка целевой ячейки, указание назначения целевой функции, указание адресов изменяемых ячеек.

• В окне Установить целевую ячейку введите адрес $E$4.

• Отметьте точкой направление целевой функции в зависимости от условий вашей задачи: в данном случае равной Максимальному значению.

• В окно Изменяя ячейки ввести адреса искомых переменных $B$2:$D$2.

5. Ввод ограничений.

• Нажмите кнопку Добавить. Появится диалоговое окно Добавление ограничения (Рисунок 7):

Рис. 7.

• В строке Ссылка на ячейку введите адрес $E$7.

• Ввести знак ограничения, в данном случае <=.

• В строке Ограничение введите адрес $G$7.

• Нажмите на кнопку Добавить.

• Аналогично введите остальные ограничения.

• После ввода последнего ограничения нажмите на кнопку ОК.

На экране появится диалоговое окно Поиск решения ( Рисунок 8).

Рис. 8.

5. Ввод параметров.

• В диалоговом окне Поиск решения нажмите кнопку Параметры. На экране появится диалоговое окно Параметры поиска решения.

• Установите флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения.

• Нажмите на кнопку ОК. На экране появится диалоговое окно Поиск решения.

• Нажмите на кнопку Выполнить.

Через короткий промежуток времени появится окно Результаты поиска решения и исходная таблица с заполненными ячейками В2:D2 для значений х_i, и ячейка E4 с максимальным значением целевой функции (Рисунок 8).

Рис. 8.

Укажите тип отчетов Результаты и Устойчивость. В результате получим на отдельных листах Отчет по результатам и Отчет по устойчивости.

На листе, на котором строилась модель появилось решение задачи: для обеспечения максимальной прибыли в размере 9000 денежных единиц необходимо произвести 400 изделий В и 550 изделий Г. Изделия А и Б производить не следует.

Ваши отчеты будут иметь вид:

Структура отчета по результатам.

В разделе Целевая ячейка указана максимальная суммарная прибыль – 1350 денежных единиц.

В разделе Изменяемые ячейки показан оптимальный план:

Х1 (количество изделий А) –430;

Х2 (количество изделий Б) – 460;

Х3 (количество изделий В) – 400;

.

В разделе Ограничения показано, что при оптимальном плане ресурсы сырья I и II используются полностью (Статус – связанное), а III недоиспользуется, о чем сообщает Статус – несвязанное.

Структура отчета по устойчивости.

В разделе Ограничения есть параметр Теневая цена, который показывает, как влияет увеличение ресурсов на единицу на увеличение значения целевой функции. Например, если увеличить запас сырья I на 200 кг, то прибыль увеличится на 3х200=600 денежных единиц.

По дефицитным видам ресурсов (полностью использованными в оптимальном плане) теневая цена больше нуля, причем самым дефицитным является тот ресурс, у которого теневая цена максимальна.

У недефицитных ресурсов (сырье III) теневая цена равна нулю.

Например, подсчитаем, как изменится суммарная прибыль (целевая функция), если запасы сырья I увеличить на 80 кг, запасы сырья II уменьшить на 10 кг. Для этого вычислим выражение:

801-102=60

То есть, в данном случае суммарная прибыль увеличится на 60 единиц.

Двумя правыми колонками задается допустимый диапазон изменения запаса ресурсов. При изменении запаса ресурсов в указанном диапазоне значение теневой цены сохраняется.

Для того, чтобы узнать, в какой ресурс следует вкладывать средства, то есть увеличить его запасы до предельного значения, нужно для каждого ресурса вычислить произведение его теневой цены на допустимое увеличение:

сырье I: 110=10 денежных единиц

сырье II: 2400=800 денежных единиц.

Заметим, что значение 1Е+30 в допустимом увеличении для сырья III свидетельствует о том, что данный параметр не влияет на целевую функцию.

Отсюда делаем вывод, что выгоднее всего вкладывать средства в закупку ресурса сырья I.

В разделе Изменяемые ячейки есть параметр Нормированная стоимость. С помощью этого параметра сравниваются затраты ресурсов на производство единицы продукции(путем умножения теневой цены на норму расхода) и прибыль от единицы продукции.

По тем видам изделий, где нормированная стоимость больше или равна нулю, делается вывод, что выпуск этих изделий предприятию выгоден (в нашем случае изделия Б, В,). Если нормированная стоимость отрицательна, то выпуск этого изделия предприятию невыгоден, и выпуск каждой единицы этого изделия снижает суммарную прибыль на указанное значение нормированной стоимости.

Затраты ресурсов на производство единицы продукции вычисляются путем умножения теневой цены каждого ресурса на нормы его расхода на единицу изделия и последующего суммирования их.. Например, для изделия х2 (изделие Б) затраты ресурсов на производство единицы продукции будут равны:

31+20+2=5

Прибыль от реализации одного изделия Б составляет 3 денежных единицы, тогда нормированная стоимость будет равна разности прибыли и затрат на одно изделие:

Прибыль-затраты=3-5 =-2

Это означает, что производство изделий Б предприятию не выгодно.

С помощью теневой цены можно исследовать вопрос о целесообразности выпуска нового вида изделия. Например, стоит ли предприятию выпускать изделие Г, о котором известно следующее:

• Прибыль от единицы этого изделия составляет 7 денежных единиц

• Затраты сырья I на изготовление одного изделия – 2,4 кг

• Затраты сырья II на изготовление одного изделия – 3 кг

Рассчитываем нормированную стоимость:

12,4+21+0=4,4 -затраты на одно изделие

7-4,4=2,6 - нормированная стоимость.

Следовательно, выпускать изделие Г предприятию не выгодно.

Три последние столбца определяют допустимый диапазон прибыли от единицы изделия. Целевая функция – это прибыль от единицы изделия.

В нашем случае прибыль от реализации одного изделия А изменяется в диапазоне от 3 до 4 денежных единиц. Прибыль от реализации одного изделия В может изменяться от 2 до 8 денежных единиц. Прибыль от реализации одного изделия Г может изменяться от 20 до 5 денежных единиц.

Если прибыль изменяется в этом диапазоне, то структура оптимального плана не меняется, изменяется только значение прибыли в целом по предприятию, то есть значение целевой функции.