20.Формулы современной величины. Обычная годовая рента

Пусть член годовой ренты равен R, процентная ставка i,

проценты начисляются один раз в конце года, срок ренты n.

Тогда дисконтированная величина первого платежа равна

Где

Приведенная к началу ренты величина второго платежа

равна Rv2

и т.д. В итоге приведенные величины образуют

геометрическую прогрессию: Rv, Rv2, Rv3, ..., Rvn, сумма кото-рой равна

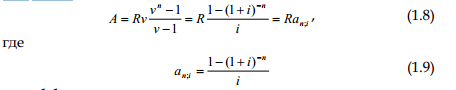
– коэффициент приведения ренты.

Как видим, коэффициент приведения ренты зависиттолько от двух параметров: срока ренты n и процентной став-ки i. Поэтому его значения могут быть представлены в таб-

личном виде. Такие таблицы можно найти в книгах или по-строить самим на компьютере.

Рента p-срочная, p ≥ 1, m ≥ 1 Аналогичные рассуждения позволяют получить форму-

лу для расчета современной величины ренты в самом общемслучае для произвольных значений p и m

от которой нетрудно перейти к частным случаям при различ-ных p и m.

21. Зависимость между современной величиной и наращенной суммой ренты

Пусть A – современная величина годовой ренты постну-мерандо, а S – ее наращенная стоимость к концу срока n, p = 1, m = 1.

Покажем, что наращение процентов на сумму A за n летдает сумму, равную S:

Отсюда же следует, что дисконтирование S дает A:

а коэффициент дисконтирования и наращения ренты связа-ны соотношениями:

22. Определение размера члена ренты.

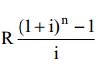
Наращенная сумма ренты: S = ;

Где R – количеств денег, вносимых каждый год на расчетный счет

i – ставка сложных процентов

n – количество лет

Отсюда размер члена ренты R = S /

23. Определение срока ренты (рента постоянная постнумерандо).

Т.к. нарощенная сумма ренты S =

Тогда количество срок ренты будет равен:

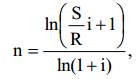
Где n – срок ренты, S – наращенная сумма, I – ставка, R - количеств денег, вносимых каждый год на расчетный счет

24. Наращенная сумма постоянной ренты постнумерандо.

Где n – срок ренты, S – наращенная сумма, I – ставка, R - количеств денег, вносимых каждый год на расчетный счет, p = число платежей в году, m = число начислений процентов в году.

25. Конверсия рент

Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом. Финансовая рента имеет следующие параметры: член ренты – величина каждого отдельного платежа, период ренты –временной интервал между двумя соседними платежами, срок ренты – время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка – ставка, используемая при наращении или дисконтировании платежей,

образующих ренту, число платежей в году, число начислений, процентов в году, моменты платежа внутри периода ренты. Существует Выкуп ренты -Выкуп ренты представляет собой замену предстоящей последовательности выплат единовременным платежом. Рассрочка платежей - это замена единовременного платежа аннуитетом.

Изменение продолжительности ренты

Пусть имеется годовая обычная рента, и у партнеров есть договоренность об изменении срока ренты, то есть вместо

срока n1, принят новый срок n2. Тогда для эквивалентности финансовых результатов требуется изменение и размера платежа. Найдем его из равенства из которого следует

Общий случай изменения параметров ренты

В случае одновременного изменения нескольких параметров ренты, исходим из равенства A1=A2. Если рассматривается годовая рента, то приводится к виду

где A1 подсчитывается заранее, t – период (возможной) отсрочки, ряд параметров задается по согласованию сторон, и один параметр находится из этого уравнения.

26. Инвестиционный проект — экономический или социальный проект, основывающийся на инвестициях; обоснование экономической целесообразности, объема и сроков осуществления прямых инвестиций в определенный объект, включающее проектно-сметную документацию, разработанную в соответствии с действующими стандартами.

Иногда для удобства выделяют понятие бизнес-плана для обозначения обоснования, при этом сам проект называют "Инвестиционный проект".

Инвестиционные проекты делятся на:

• производственные

• научно-технические

• коммерческие

• финансовые

• экономические

• социально-экономические

В коммерческой практике принято выделять:

а) инвестиции в финансовые активы (реальные, или капиталообразующие, или производственные инвестиции) — инвестиции в производственные здания и сооружения, любые виды машин и оборудования сроком службы более одного года;

б) инвестиции в денежные активы (портфельные инвестиции) — права на получение денежных сумм от других юридических или физических лиц;

в) инвестиции в нематериальные активы — расходы, не связанные с материальным воплощением, но имеющие экономическую ценность. Могут быть материализованы в случае ликвидации предприятия, а также при слиянии и поглощении.