Расчет срока ссуды при начислении по сложным процентным ставкам.
При наращении по сложной годовой ставке i и по номинальной ставке j на основе формул S=P(1+i)n и S=P(1+j/m)mn получим:
,
(3.18)
. (3.19)
При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f из P=S(1-d)n и P=S(1-f/m)mn получим:
,
(3.20)
.
(3.21)
Расчет величины процентной ставки (сложные проценты).
При наращении по сложной годовой ставке процентов i и по номинальной ставке j из формул S=P(1+i)n и S=P(1+j/m)mn получим:
, (3.22)
. (3.23)
При дисконтировании по сложным учетным ставкам d и f из формул P=S(1-d)n и P=S(1-f/m)mn:
, (3.24)
, (3.25)
Дисконтирование по сложной учетной ставке
В практике учетных операций иногда применяют сложную учетную ставку. В этом случае процесс дисконтирования происходит с замедлением, поскольку на каждом шаге учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени.
Дисконтирование по сложной учетной ставке выполняется по формуле:
, (3.14)
где d – сложная годовая учетная ставка.
Номинальная и эффективная учетные ставки
Дисконтирование
может производиться не один раз в году,
а m раз в год, т. е. каждый раз учет
производится по ставке
.
В этом случае
, (3.15)
где f – номинальная годовая учетная ставка.
Эффективная учетная ставка d показывает степень дисконтирования за год. Ее определяют из равенства дисконтных множителей:
,
откуда
.
В
свою очередь
.
Эффективная учетная ставка меньше номинальной при m > 1.
Наращение по учетной ставке.
Иногда наращенную сумму получают и с помощью сложной учетной ставки. Из (3.14) и (3.15) следует:
,
.
Начисление процентов в условиях инфляции. (простые проценты)
Инфляцию необходимо учитывать, по крайней мере, в двух случаях: при
расчете наращенной суммы денег и при измерении реальной эффективности
(доходности) финансовой операции. Остановимся на этих проблемах. Введем
следующие обозначения:
S — наращенная сумма денег, измеренная по номиналу;
С — наращенная сумма с учетом ее обесценивания за счет инфляции;
JP — индекс цен, величина, показывающая, во сколько раз возросли цены за
анализируемый период;
α – темп инфляции (относительный прирост цен за анализируемый период);
r – номинальная ставка процента;
i – эффективная ставка процента.
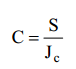
Если инфляция постоянна на протяжении нескольких периодов времени (a = const ),
то индекс цен за n периодов (месяцев, лет и т.д.) определяется по формуле:
если же инфляция изменяется со временем (a ¹ const ), то
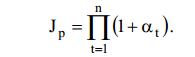
наращенная сумма с учетом снижения покупательной способности равна
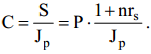
При условии a = const получим
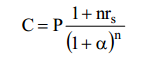
Начисление процентов в условиях инфляции. (сложным проценты)
См. выше.
Если наращение производится по сложной ставке, то наращенная сумма с
учетом инфляции равна
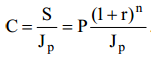В
этом случае увеличение наращенной суммы
с учетом ее инфляционного обесценивания
имеет место только тогда, когда
При
условии a = const получим
