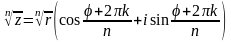27. Тригонометрический ряд Фурье. Разложение четных и нечетных функций в тригонометрический ряд Фурье.

Тригонометрические ряды (ряды Фурье) периодической функции периода .

Тригонометрическим рядом называется ряд вида

.

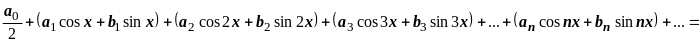
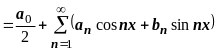Условия сходимости этого ряда мы сформулируем дальше, сейчас предположим, что этот ряд сходится в любой точке, и что его сумма равна . Очевидно, что - периодическая функция периода (как сумма периодических функций). Выразим коэффициенты ряда через функцию . Умножая скалярно равенство на 1, получим

. Так как 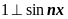, , то все слагаемые в сумме равны нулю, поэтому , или . Умножим то же равенство скалярно на , в результате . Здесь равны нулю все скалярные произведения, кроме скалярного квадрата функции (в сумме при ), поэтому .

Умножая равенство на , получим . Окончательно

.

(параметр переобозначен ).

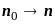Таким образом, если периодическая функция периода является суммой тригонометрического ряда, то коэффициенты этого ряда выражаются через функцию полученными формулами.

Теорема Дирихле

Пусть функция периода удовлетворяет следующим условиям:

1. непрерывна на интервале всюду, за исключением конечного числа точек разрыва первого рода (т.е точек, в которых существуют конечные пределы слева 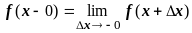и справа 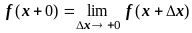, не равные друг другу);

2. Имеет на этом интервале конечное число экстремумов.

Тогда ряд Фурье сходится в каждой точке отрезка . Его сумма равна

в точках непрерывности этой функции;

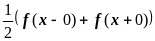в точках разрыва этой функции;

в точках .

Коэффициенты ряда Фурье чётных и нечётных функций. Если - чётная функция, то произведение - функция нечётная, и по известному свойству определённого интеграла от нечётной функции, . Мы проверили это на примере функции 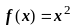. Произведение в этом случае - функция чётная, поэтому . Итак, для чётных функций .

Если - нечётная функция, то произведение - функция нечётная, поэтому . Произведение - функция чётная, поэтому . Итак, для нечётных функций

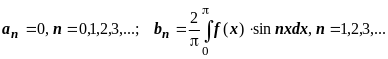
28. Комплексные числа: основные определения, действия с ними.

Выражение вида z=x+iy, где x, y– действительные числа, а i²=1, называется комплексным числом.

x – действительная часть и обозначается Rez=x (real), y – мнимая часть, обозначается Imz=y (imation).

Два комплексных числа называются равными, если равны между собой их действительные и мнимые части.

Комплексное число можно изобразить в виде точки декартовой координатной плоскости, причем координата x – действительная часть, координата y – мнимая часть, соответственно – действительная и мнимая оси. Изображение комплексного числа может быть так же задано с помощью радиус – вектора, т.е.

Очевидно, что и называется модулем комплексного числа, а называется аргументом комплексного числа, причем аргумент комплексного числа имеет период в общем виде выглядит так: , где argz – главное значение.

Если совместить декартовую систему координат с полярной осью, получим: Комплексные числа можно представить в формах:

z=x+iy – алгебраическая запись комплексного числа. - тригонометрическая запись комплексного числа. - показательная или экспоненциальная запись комплексного числа.

Арифметические действия с комплексными числами.1. Сложение. 2. Вычитание.

Разность и сумму выполнять лучше в алгебраической форме.3. Умнож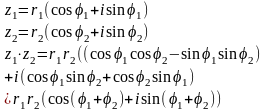ение. 4. Деление

5. Возведение в степень.