1. Функции нескольких переменных. Линии и поверхности уровня.

Функции нескольких переменных.

Переменная z(с областью изменения Z)называется функцией двух независимых переменныхх,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.Обозначение: z = f(x,y).Примеры:

1. z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.

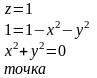2. - функция, областью определения которой являются решения неравенства .

Переменная z(с областью изменения Z)называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел 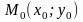из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.Обозначение: z = f Линии и поверхности уровня.Линии уровня функции z = f(x,y) называется линия на плоскости f(x,y)=С, т.е.линия, в которой функция принимает постоянное значение.Окружность – линии уровная при z равно какому-то значению.Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.Пример.Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y – 7z –12 + с = 0.

2. Предел и непрерывность функции нескольких переменных.

Предел функции нескольких переменных

Для функции двух (и большего числа) переменных вводится понятие предела функции и

непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности

точки. Множество всех точекМ(х;у) плоскости, координаты которых удовлетворяют неравенству называется δ-окрестностью точки Мо(хо;уо). Другими словами, δ-окрестность точки - это все внутренние точки круга с центром Мо и радиусом δ.

Пусть функция z = f(х; у) определена в некоторой окрестности точки Мо(хо;уо), кроме, бытьможет, самой этой точки. Число А называется пределом функции z = f(х;у) при х →хо и у→ уоили, что то же самое, при М(х;у) → М₀(хо;уо), если для любого ε > 0 существует δ > Отакое,что для всех х≠х0 и у≠y0 и удовлетворяющих неравенству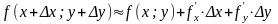 выполняется неравенство|f (x; у) — А| <ε. Записывают:

Непрерывность и точки разрыва

Функция z = f(х; у) (или f(М)) называется непрерывной в точке Мо(хо; уо), если она:

а) определена в этой точке и некоторой ее окрестности,

б) имеет предел ,

в) этот предел равен значению функции z в точке Мо, т. е. , или

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.

Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=f(x; у) могут образовывать целые линии разрыва, а иногда и более сложные геометрические образы.