1) Мода;

2) Среднее арифметическое значение;

3) Медиана.

• Мода ( или Мo) - это наиболее часто встречающееся значение в ряду данных.

• Например, в следующем массиве:

{2, 3, 5, 1, 4, 5, 6, 5, 2}

модой будет являться значение 5 (обозначается следующим образом: Мо = 5). Если выборка содержит две моды, то распределение называется бимодальным.

Таким примером может служить массив

{3, 3, 5, 1, 4, 5, 6, 5, 3} (Мo1 = 5, а Мo2 = 3).

Если все значения выборки встречаются одинаково часто, то моды у распределения нет. Бимодальное или полимодальное (содержащее более двух мод) распределения могут рассматриваться как признак неоднородности выборки.

Например, школьный класс образован в результате механического слияния двух разных классов, и показатели мод интеллекта были изначально различны. После слияния в объединенной выборке график интеллекта будет иметь две моды.

Моду проще всего выявить графически, построив ему значение и будет модой (см. рисунок). гистограмму частотного распределения показателей и найдя на ней пик или (равновеликие пики) –соответствующее

Среднее арифметическое значение (или просто среднее) ( или М или Мx) это отношение суммы всех значений данных к числу слагаемых. Число слагаемых (то есть объем выборки) обозначается буквой п (или N), а индивидуальные значения показателя - символом x_i.

• Среднее арифметическое позволяет «уравновесить» отклонения всех величин и представить типичное значение, характеризующее выборку. Основной недостаток это чувствительность к «выбросам» - слишком большим или малым значениям по сравнению с другими. В качестве примера можно рассмотреть массив:

• {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20}.

• Мх= =(8 + 9+ 11 +2×12 + 13 + 14+ 17 + 2×19 + 2×20) / 12 = 14,5.

• Если в ряду данных присутствуют числа со знаком «минус», то суммирование производится с учетом этих знаков.

Медиана (Ме) разбивает выборку на две равные части, 50% значений ряда больше медианы и столько же меньше.

• Для определения медианы рекомендуется сначала упорядочить данные.

• Например, для определения значения медианы в массиве

{8, 11, 12, 20, 12, 13, 9, 15, 19, 17, 19} необходимо этот массив упорядочить (произвести сортировку по возрастанию):

{8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20}.

Медиана будет равна 13 (обозначается следующим образом: Ме = 13). Если количество данных в выборке четное, то медиана равна среднему арифметическому показателю между двумя центральными значениями.

Например, если добавить в последнюю выборку значение 20, то упорядоченный массив примет следующий вид:

{8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20, 20}.

Медиана будет равна 14. В подобном случае медиана не может соответствовать ни одному из значений выборки. Медиана может принимать и дробные значения.

Например, если мы в последнем примере 15 (одно из двух центральных значений) заменим на 14, то массив примет вид

{8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20}

и медиана будет равна 13,5.

Применение мер центральной тенденции

• Мода. В общих случаях моде присущи недостатки:

• 1. Она дает меньше информации, чем любое другое измерение.

• 2. Во многих случаях она может отсутствовать.

• 3. При сгруппированных данных она зависит от выбранной границы интервала.

• 4. Нет других статистических вычислений, которые бы на ней основывались.

• В то же время мода имеет некоторые преимущества.

• 1. Она быстро дает представление о типичном по группе. На ее основе можно утверждать, что «эта вещь случается чаще, чем все другие».

• 2. Она малочувствительна к экстремальным значениям (значениям крайне высоким и крайне низким).

• 3. Ее очень легко посчитать.

• Есть две ситуации, в которых предпочтительно использовать моду, нежели медиану или среднее.

• Первый случай - мультимодальное распределение. В этом случае вычисленные среднее и медиана не дадут адекватного представления о характеристиках распределения (если предположения о типичном делаются, ориентируясь на среднее и медиану, то допускается серьезная ошибка).

• Вторая ситуация, в которой предпочтительно использовать именно моду, — это когда можно (нужно) сформировать только один класс объектов. Если коммивояжер взял с собой только одну пару демонстрируемой обуви, будет лучше, если он возьмет пару самого ходового размера, чем пару, представляющую «моду» среди всех размеров, или пару среднего размера. Продавец понимает, что лучше взять то, что соответствует размеру ноги большинства людей.

• Медиана. Хотя и является лучшей мерой, чем мода, но тоже имеет определенные недостатки.

• 1. Бесполезна при бимодальном (вообще мультимодальном) распределении.

• 2. Не участвует в дальнейших статистических вычислениях. Медиана имеет и определенные преимущества.

• 1. Часто дает достаточное описание «типичного» случая, исключая вариант мультимодальнего распределения.

• 2. Относительно не подвержена влиянию экстремальных значений в случае, когда небольшое их количество искажает «среднюю» картину.

• Среднее. В общем случае среднее имеет больше преимуществ перед модой и медианой.

• 1. Это единственная мера центральной тенденции, которая использует всю информацию, содержащуюся в данных.

• 2. Относительно независима от размера и стартовой точки интервала (при сгруппированных данных).

• 3. Ее легко посчитать, и, что более важно, она используется как стартовая точка для дальнейшей статистической обработки (для вычисления стандартного отклонения, коэффициента корреляции и для множества других статистик).

• Основной недостаток среднего - чувствительность к экстремальным значениям изучаемого распределения.

• В целом можно сказать, что среднее - более предпочтительно по сравнению с медианой, а медиана - по сравнению с модой. Но если надо описать данные наилучшим образом, начать следует с подсчета всех 3-х мер центральной тенденции для полученного распределения.

8. Меры положения.

• Кроме мер центральной тенденции в психологии широко используются меры положения, которые называются квантилями распределения.

• Квантиль – это точка, на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на 2 группы с известным соотношением их численности (в заданной пропорции). Один из квантилей – медиана. Кроме медианы часто используются процентили и квартили.

• Процентили (Percentiles) – это 99 точек – значений признака (P1, …, P99), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности. Десятый процентиль P10 соответствует тому значению признака, который отделяет эти 10% испытуемых от остальных 90%.

• Квартили – (Quartiles) – это 3 точки – значения признака (P25, P50, P75), которые делят упорядоченное (по возрастанию) множество наблюдений на 4 равные по численности части (или в пропорции i/4 от нижнего значения к верхнему). Первый квартиль соответствует 25-му процентилю, второй – 50-му процентилю или медиане, третий квартиль соответствует 75-иу процентилю.

• Процентили и квартили используются для определения частоты встречаемости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений.

9. Меры изменчивости.

Наиболее часто используемые - размах, дисперсия, стандартное отклонение.

Размах (R) - это разница между максимальным и минимальным значениями.

R = .

Размах обычно определяют после процедуры упорядочивания.

Среднее отклонение. Смысл среднего отклонения заключен в его названии. Это среднее отклонение показателей от какого-то значения, обычно от среднего арифметического по выборке. Знак отклонения в этом случае игнорируется.

где AD - среднее отклонение;

- абсолютная величина различия между некоторым показателем и средним;

п - число случаев в выборке.

Среднее отклонение будет очень удобной мерой, если не нужно производить дальнейших подсчетов. Но если используются более сложные (что и происходит в подавляющем большинстве случаев), то эта мера бесполезна - гораздо лучше будет воспользоваться стандартным отклонением.

Дисперсия (D, SD² или σ²) - это мера разброса данных относительно среднего значения, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего.

Чем больше изменчивость данных, тем больше отклонения от среднего, тем больше величина дисперсии.

Преимущество дисперсии в том, что при её подсчёте учитывается каждое значение, однако количество значений роли не играет - можно сравнивать дисперсию 2-х выборок различного размера!!!

Стандартное отклонение (обозначается как SD или σ) для оценок, полученных на выборке, - это среднее значение, на которое эти оценки отклоняются от среднего арифметического.

x_i – сырой показатель;

– среднее арифметическое по выборке;

n – число случаев в выборке.

Стандартная ошибка

Стандартное отклонение представляет собой квадратный корень из дисперсии. По ряду причин этот показатель является более удобным, чем дисперсия (всегда квадрат исходной величины).

Стандартное отклонение используется в более сложных статистиках, и оно принципиально важно для понимания того, как тест устроен и как тест создается.

Всегда полезно держать в голове смысл и предназначение того или иного правила. В случае со стандартным отклонением роль этой меры переоценить сложно.

применение стандартного отклонения - с его помощью высчитывается «коридор нормы», или «нормативный коридор ».

Коэффициент вариации

10. Понятие нормального распределения и его параметры.

Предположим, что исследователь собирается изучить некий показатель выборки, про который известно, что он принимает в основном средние значения, а очень высокие или очень низкие значения встречаются достаточно редко (например, рост испытуемых). Результаты своего исследования он будет изображать в виде частотной диаграммы, позволяющей судить о распределении значений в выборке.

В том случае, если число испытуемых будет составлять несколько сотен или тысяч человек, то диаграмма распределения будет всё более походить на изображенную на рис. 1.

Подобное распределение значений показателя принято называть нормальным, а получившаяся кривая носит название кривой нормального распределения. Оно применимо только для метрических величин!

Эмпирическим путем было установлено, что многие биологические параметры распределены подобным образом (рост, вес и так далее). Впоследствии психологи выяснили, что и большинство психологических свойств (показатели интеллекта, темпераментных особенностей, способностей и других психических явлений) также имеют нормальное распределение. Считается, что нормальное распределение представляет собой нечто вроде «идеала» природы, когда при наличии небольшого числа чрезмерно высоких и чрезмерно .низких показателей большая часть значений находится в рамках среднего. Этот принцип учитывается при стандартизации тестовых методик. При этом, чем больше объем выборки, тем достовернее полученное эмпирическое распределение приближается к нормальному. Нормальным распределением может быть только распределение с числом наблюдений не менее 30.

• Это распределение описывается формулой:

• Нормальное распределение обладает следующими свойствами;

• - в диапазоне М±σ находится 68,26% всех значений показателя;

• - в диапазоне М±2σ находится 95,44% всех значений показателя;

• - в диапазоне М±3σ находится 99,72% всех значений показателя.

• Помимо этого, значения моды, медианы и среднего арифметического в выборке, распределённой по нормальному закону, совпадают.

Следовательно, если известно, что распределение исследуемого показателя близко к нормальному, то можно утверждать, что в диапазоне М ± σ окажутся значения более чем двух третей испытуемых, а за пределами диапазона М ± 3σ будут находиться так называемые «выбросы» - чрезмерно отличающиеся показатели, которые могут быть ошибочными. В том случае, если не предполагается анализ чрезмерно отклоняющихся значений, исследователь может ограничиться данными, находящимися в диапазоне, размах которого составляет одно или два стандартных отклонения от среднего значения (М ± σ или М ± 2σ). Информация о том, является ли распределение показателя в группе близким к нормальному или нет, оказывает значительное влияние на выбор методов

Принято считать, что в пределах М ± 2σ располагаются значения, относящиеся к статистической норме математико-статистического анализа данных, то есть те значения, которые включены в так называемый 95%-ный доверительный интервал. Знание М и σ можно использовать для выведения статистической нормы.

• Обязательные для этой процедуры условия: соответствие распределения нормальному и п > 30.

• Например, необходимо определить границы нормы для российской выборки у переведенного недавно с английского языка теста. После перевода и адаптации мы проводим исследование на студентах, чьим родным языком является русский. По окончании обработки результатов получаем: п = 80, М = 30, σ = 5,9. Границы статистической нормы для теста лежат в диапазоне М ± 2σ, то есть 30 ± 11,8. Таким образом, верхняя граница нормы =42, нижняя = 18.

11. Проверка нормальности распределения.

Рассматриваемые в следующих лекциях параметрические критерии можно использовать только в том случае, если исследуемые данные подчиняются закону нормального распределения. В связи с этим часто возникает вопрос: как проверить характер распределения данных? Для этого необходимо определить асимметрию и эксцесс.

Принцип принятия или отвержения гипотезы о нормальности распределения является следующим:

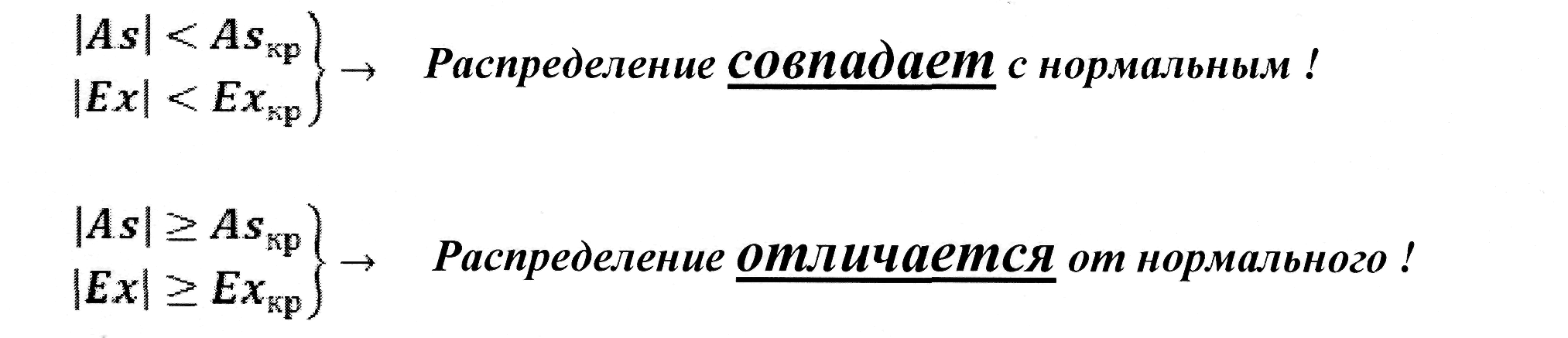
Асимметрия — это показатель симметричности/скошенности кривой распределения.

При левосторонней асимметрии ее показатель является положительным и в распределении преобладают более низкие значения признака. При правосторонней - показатель отрицательный и преобладают более высокие значения. У всех симметричных распределений (в том числе и у нормального распределения) значение асимметрии равно нулю. Формула показателя асимметрии следующая:

Эксцесс определяет плосковершинность или остроконечность кривой распределения.

Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения две вершины (бимодальное распределение), то его эксцесс стремится к отрицательной величине. Показатель эксцесса определяется по формуле:

Сравнение эмпирического распределения с теоретическим нормальным -важнейшая процедура, которая должна использоваться при стандартизации любого теста. Результаты такого сравнения могут показать (и это очень желательно для создателя теста), что полученное эмпирическое распределение не отличается значимо от теоретического. Такой результат говорит о том, что тест качественный в смысле уровня сложности задач, из которых он состоит, их достаточности, а также о том, что выборка стандартизации соответствует характеристикам популяции.

Есть еще одна причина, по которой исследователи стремятся получить распределение, близкое к нормальному, - в этом случае полученные данные можно подвергать самым разным видам статистического анализа, что было бы невозможно в случае ненормального распределения!

12. Нормальное распределение. Условия, влияющие на форму графика распределения.

Нормальное распределение обладает следующими свойствами;

- в диапазоне М±σ находится 68,26% всех значений показателя;

- в диапазоне М±2σ находится 95,44% всех значений показателя;

- в диапазоне М±3σ находится 99,72% всех значений показателя.

Помимо этого, значения моды, медианы и среднего арифметического в выборке, распределённой по нормальному закону, совпадают.

Принято считать, что в пределах М ± 2σ располагаются значения, относящиеся к статистической норме.

Распределение считается не нормальным, если эмпирический результат абсолютной величины показателей асимметрии и эксцесса превышает их критические значения или равен им.

Графики распределений, существенно отличающиеся от нормальных и проявляющие одну или несколько характеристик, описанных выше, время от времени появляются у исследователей (рис.2).

Это происходит, когда:

- используются неадекватная выборка,

- неудачные или непригодные средства измерения,

- существуют некоторые факторы, воздействующие непосредственно на исследуемое качество.

Используются неадекватная выборка.

Скошенность проявляется, если в состав выборки вошли две группы, имеющие выраженные отличия по измеряемому признаку. Например, при измерении умственных способностей у детей в школах интернатного типа есть вероятность получения скошенного графика распределения (рис. 3).

Рис.3. Скошенное распределение данных, полученных на выборке, состоящей из 2-х различных групп

Мы видим, что низкие оценки умственных способностей представляют большинство от всех оценок по выборке. Такая асимметрия связана с тем, что в школах-интернатах могут находиться две группы детей, отличающихся по умственным способностям: нормальные дети и дети с задержкой психического развития. Если бы исследователь измерил умственные способности у этих двух групп детей по отдельности, то он получил бы два нормальных графика распределения с разными средними арифметическими.

Если в выборку включены люди разных уровней развития, то может быть получено бимодальное распределение (рис. 4).

Если эксцесс Ех<0 явно выражен (рис.5), то это может происходить из-за гомогенности людей, включённых в выборку.

Следствием тестирования малых групп часто является «зубчатый» вид графика - так проявляются индивидуальные значения (рис.6).

Чем больше будет выборка, тем более гладким станет график распределения.

13. Стандартизация и шкальные преобразования экспериментальных данных.

Аналогично изученной процедуре ранжирования (определённый порядок сортировки значений, представленных в числовой шкале, как правило, ранговой, состоящий в особой перегруппировке данных, которая позволяет упорядочить показатели от наименее выраженных до наиболее выраженных с сохранением порядка) в некоторых случаях, сырые баллы при помощи линейного преобразования по специальной формуле или таблице переводятся (пересчитываются) в стандартизированные оценки. Это делается для того, чтобы привести распределение значений шкалы как можно ближе к нормальному распределению. Таким образом, появится возможность оценивать показатели, включающие в себя разное количество пунктов.

Часто такое преобразование выполняется отдельно для мужчин и женщин, для лиц различного возраста и разных профессиональных групп и т.п. Наличие стандартизированных оценок для разных половозрастных и профессиональных категорий испытуемых указывает на профессиональный подход исследователей к разработке и апробации методики.